1. Gibbs 에너지의 극소
3-3장에서 설명한 것 처럼 일정한 온도와 압력 하에서 자발적 변화는 Gibbs 에너지가 낮아지는 쪽으로 일어남
반응 혼합물의 경우 그 혼합물의 Gibbs 에너지가 극소치에 도달할 때까지 반응을 일으키는데 이때가 바로 평형 상태임
이때는 정반응과 역반응이 같은 속도로 진행하는 동적 상태임
https://nate0707.tistory.com/80
【물리화학1】 3-3 계를 주목할 때
0. 이전이야기 이전 포스팅에서는 엔트로피의 측정에 대하여 다뤘음엔트로피를 측정할 때는 대기압에서의 측정을 가정하며 각 구간에서의 상전이 엔트로피를 고려해줘야함$S_m(T)=S_m(0)$ $+\int_0^{
nate0707.tistory.com
반응 혼합물의 Gibbs 에너지를 계산한 후 이것이 최소가 될 때의 조성을 알아낸다면, 그 반응 혼합물의 평형 조성을 알 수 있음
- 반응 Gibbs 에너지
Gibbs 에너지 변화는 반응 진척도 $\xi$를 이용해 나타낼 수 있음
* 이때 반응 진척도는 물질량의 디멘션을 가지며 몰수로 나타냄
$A \rightleftharpoons B$에서
$dG=\mu_Adn_A+\mu_Bdn_B=-\mu_Ad\xi+\mu_Bd\xi=(\mu_B-\mu_A)d\xi$
이 식을 정리하면 다음과 같음
$\Delta_r G=\mu_B-\mu_A=(\frac{\partial G}{\partial \xi})_{p, T}$ 반응 Gibbs 에너지
즉, $\Delta_r G$는 반응 혼합물의 현재 조성 상태에서의 반응물과 생성물들 사이의 화학 퍼텐셜의 차이임
화학 퍼텐셜은 조성에 따라 변하므로 Gibbs 에너지의 반응 진척도에 따른 기울기도 반응이 진행함에 따라 변함
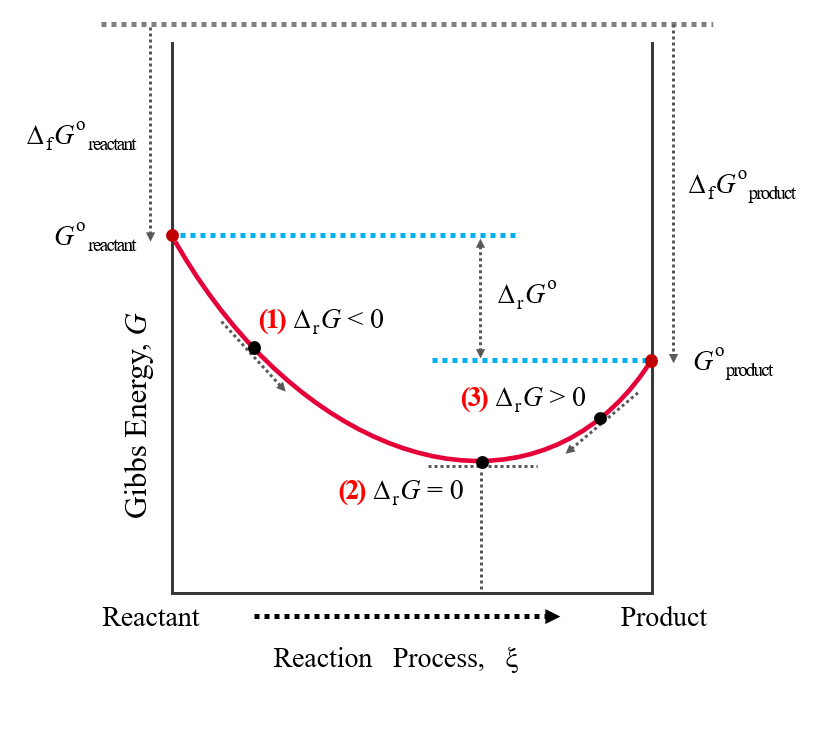
(1) $\Delta_r G<0$인 경우 $\mu_B<\mu_A$이고 정방향의 반응이 자발적임
(2) $\Delta_r G=0$인 경우 $\mu_B=\mu_A$이고 반응이 평형 상태임
(3) $\Delta_r G>0$인 경우 $\mu_B>\mu_A$이고 역방향의 반응이 자발적임
- 일-생산성과 일-소모반응성 반응
$\Delta_r G<0$인 반을을 일-생산성이라고 함, exergonic, 반응이 자발적이므로 화학 반응을 일어나게 하거나 비-팽창 일을 함
$\Delta_r G>0$인 반응을 일-소모성이라고 함, endergonic, 반응이 비자발적이므로 여기에 일을 해줌으로써 자발적 생성 반응을 일으킴
2. 평형의 설명
- 완전 기체 평형
A와 B가 완전 기체일 때는 $\mu=\mu^{\theta}+RTlnp$를 이용하여 반응 Gibbs 에너지를 쓸 수 있음
* 이때 $p=p/p^{\theta}$
$\Delta_r G=\mu_B-\mu_A=(\mu_B^{\theta}+RTlnp_B)-(\mu_A^{\theta}+RTlnp_A)=\Delta_r G^{\theta} +RTln\frac{p_B}{p_A}$
이때 부분 압력들의 비를 Q로 나타내면
$\Delta_r G=\Delta_r G^{\theta}+RTlnQ$ $Q=\frac{p_B}{p_A}$
이때 $\Delta_r G^{\theta}$는 순수한 A,B의 Gibbs 에너지 차이를, $RTlnQ$는 두 물질이 섞일 때 반응이 진행되는 정도를 나타냄
* $\Delta_r G^{\theta}=G_m^{\theta}(B)-G_m^{\theta}(A)=\mu_B^{\theta}-\mu_A^{\theta}$로 반응물과 생성물의 표준 몰 Gibbs 에너지 차이를 말함
* 표준 반응 Gibbs 에너지는 표준 생성 에너지를 이용해서 나타내기도 함 $\Delta_r G^{\theta}=\Delta_f G^{\theta}(B)-\Delta_f G^{\theta}(A)$
이때 평형에서 $\Delta_r G=0$이고 평형에서의 부분 압력들의 비는 K로 나타냄
$0=\Delta_r G^{\theta}+RTlnK$
$RTlnK=-\Delta_r G^{\theta}$ $K=(\frac{p_B}{p_A})_{equil}$
* K가 크다는 것은 $p_B>>p_A$의 뜻으로 정반응이 많이 일어났다는 것임
# 혼합을 고려할 때와 무시할 때의 반응 진척도와 Gibbs 에너지 그래프
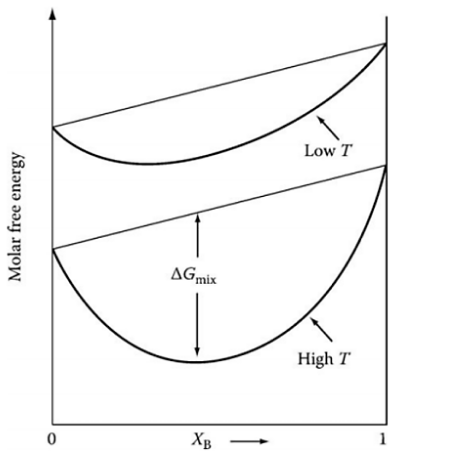
$G=H-TS$에서 혼합을 고려하지 않고, 즉 S 엔트로피를 고려하지 않을 때는 H에 따라서 G값이 선형적으로 변함
하지만 혼합을 고려한다면 $\Delta_{mix} G=nRT(x_Alnx_A+x_Blnx_B)$의 기여를 Gibbs 에너지에 포함시켜야 함
그렇기에 위와 같은 그래프가 그려짐
이때도 마찬가지로 극소치에서 평형을 이룸
# 평형일때의 표준 반응 에너지 $\Delta_r G^{\theta}$의 부호
$\Delta_r G^{\theta}>0$일 때는 K<1 이며 $p_B<p_A$가 되어 반응물 A가 우세함을 뜻함
$\Delta_r G^{\theta}<0$일 때는 K>1 이며 $p_B>p_A$가 되어 생성물 B가 우세함을 뜻함
- 일반적 반응의 경우
지금까지는 $A \rightleftharpoons B$의 반응에 대해서만 이야기 했음
이제는 일반적 반응에 이를 확대해 적용할 것임
우선 $2A+B \rightleftharpoons 3C+D$의 일반적인 반응을 다음과 같이 표현할 수 있음
$0=\sum_J v_JJ$
* 이때 $v_J$는 화학종 J의 화학량적 수
$\Delta_r G=\Delta_r G^{\theta}+RTlnQ$ 일반적 반응에서의 반응 Gibbs 에너지
* 일반적 반응에서도 반응 Gibbs 에너지식은 똑같음
* 하지만 이때 $\Delta_r G^{\theta}$와 $RTlnQ$에 해당하는 값이 달라짐
$\Delta_r G^{\theta}=\sum_{products} v\Delta_f G^{\theta}-\sum_{reactatns} v\Delta_f G^{\theta}$ 표준 반응 Gibbs 에너지
이를 간편하게 나타내면 다음과 같음
$\Delta_r G^{\theta}=\sum_J v\Delta_f G^{\theta}(J)$
반응 가중비 Q는 다음과 같은 꼴로 표시됨
$Q=\frac{생성물 활동도}{반응물 활동도}$
여기서 활동도는 각종들의 것을 화학량적 수만큼씩 가중곱을 취한 것으로 곱셈 기호 $\prod$ 를 이용함
$Q= \prod_J a_J^{v_J}$
# 예시
$2A+3B→C+2D$ 반응에서 $Q=\frac{a_Ca_D^2}{a_A^2a_B^3}$
평형에서 G의 기울기는 0이므로 $\Delta_r G=0$ 이때의 활동도가 평형 상수 K임
$K=(\prod_J a_J^{v_J})_{equil}$ 평형 상수의 정의
$\Delta_r G^{\theta}=-RTlnK$ 열역학적 평형 상수
* 열역학적 평형 상수를 이용하면 임의의 반응에 대한 평형 상수를 계산할 수 있고 또한 평형 조성도 예측할 수 있음
- 평형 상수들 사이의 관계
평형 상수를 논할때, 활동도를 그대로 사용하기 보다는 농도와 연관시켜 사용하는 경우가 많음
$a_J=\gamma_Jx_J$, $a_J=\gamma_J b_J/b^{\theta}$, $a_J=[J]/c^{\theta}$를 이용해야 함
* 이때 셋 중 어떤 것을 이용하느냐에 따라 $\gamma_J$값이 달라질 수 있음
* 여기서 $x_J$는 몰분율, $b_J$는 몰랄 농도, [J]는 몰농도임
이때 평형상수를 농도와 연관시키면 다음과 같은 식이 유도됨
$K=K_c \times (\frac{c^{\theta}RT}{p^{\theta}})^{\Delta V}$
이때 괄호 안의 값은 T/(12.03K)가 됨
- 평형 상수의 분자 수준 해석
평형 상수와 Boltzmann 분포 법칙을 연관시켜 이야기할 수 있음
원자들은 두 에너지 준위 세트를 구분하지 않고 모든 준위에 Boltzmann 분포 법칙에 따라 분포되는데, 온도가 주어지면 그 온도에 고유한 개체수 분포가 나타나며 반응 혼합물이 고유한 조성을 가지게 되는 것임
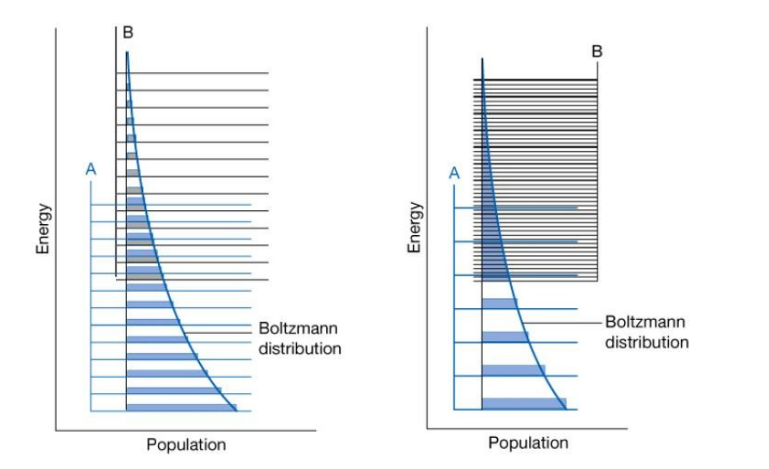
* 이때 두 가지 그림 모두 흡열 반응 $A→B$를 나타낸 것임
첫 번째 그림의 경우 생성물과 반응물의 에너지 준위가 비슷함
G=H-TS 에서 S의 변화가 0이므로 G<0이 되기 위해서 H<0이 되어야 함
두 번째 그림의 경우 B의 에너지 준위 밀도가 A의 에너지 준위 밀도에 비해 매우 큼
A에서 B로 반응할 때 S>0이고 H<0이므로 G<0임
이때 $\Delta_r G^{\theta} =\Delta_r H^{\theta}-T\Delta_r S^{\theta}$ 와 $\Delta_r G^{\theta}=-RTlnK$ 를 이용하면
$K=e^{-\Delta_r H^{\theta}/RT}e^{\Delta_r S^{\theta}/R}$
만약 흡열 반응, 즉 $\Delta_r H^{\theta}>0$이면 $e^{-\Delta_r H^{\theta}/RT}$는 0에 가까워지고 즉 $\Delta_r S^{\theta}$에 의해 K값이 결정 됨
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 6-2 평형에 영향을 주는 요인 (0) | 2024.09.21 |
|---|---|
| 【물리화학1】 6장 화학 평형 (1) | 2024.09.20 |
| 【물리화학1】 5-6 이온의 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-5 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
1. Gibbs 에너지의 극소
3-3장에서 설명한 것 처럼 일정한 온도와 압력 하에서 자발적 변화는 Gibbs 에너지가 낮아지는 쪽으로 일어남
반응 혼합물의 경우 그 혼합물의 Gibbs 에너지가 극소치에 도달할 때까지 반응을 일으키는데 이때가 바로 평형 상태임
이때는 정반응과 역반응이 같은 속도로 진행하는 동적 상태임
https://nate0707.tistory.com/80
【물리화학1】 3-3 계를 주목할 때
0. 이전이야기 이전 포스팅에서는 엔트로피의 측정에 대하여 다뤘음엔트로피를 측정할 때는 대기압에서의 측정을 가정하며 각 구간에서의 상전이 엔트로피를 고려해줘야함$S_m(T)=S_m(0)$ $+\int_0^{
nate0707.tistory.com
반응 혼합물의 Gibbs 에너지를 계산한 후 이것이 최소가 될 때의 조성을 알아낸다면, 그 반응 혼합물의 평형 조성을 알 수 있음
- 반응 Gibbs 에너지
Gibbs 에너지 변화는 반응 진척도 $\xi$를 이용해 나타낼 수 있음
* 이때 반응 진척도는 물질량의 디멘션을 가지며 몰수로 나타냄
$A \rightleftharpoons B$에서
$dG=\mu_Adn_A+\mu_Bdn_B=-\mu_Ad\xi+\mu_Bd\xi=(\mu_B-\mu_A)d\xi$
이 식을 정리하면 다음과 같음
$\Delta_r G=\mu_B-\mu_A=(\frac{\partial G}{\partial \xi})_{p, T}$ 반응 Gibbs 에너지
즉, $\Delta_r G$는 반응 혼합물의 현재 조성 상태에서의 반응물과 생성물들 사이의 화학 퍼텐셜의 차이임
화학 퍼텐셜은 조성에 따라 변하므로 Gibbs 에너지의 반응 진척도에 따른 기울기도 반응이 진행함에 따라 변함

(1) $\Delta_r G<0$인 경우 $\mu_B<\mu_A$이고 정방향의 반응이 자발적임
(2) $\Delta_r G=0$인 경우 $\mu_B=\mu_A$이고 반응이 평형 상태임
(3) $\Delta_r G>0$인 경우 $\mu_B>\mu_A$이고 역방향의 반응이 자발적임
- 일-생산성과 일-소모반응성 반응
$\Delta_r G<0$인 반을을 일-생산성이라고 함, exergonic, 반응이 자발적이므로 화학 반응을 일어나게 하거나 비-팽창 일을 함
$\Delta_r G>0$인 반응을 일-소모성이라고 함, endergonic, 반응이 비자발적이므로 여기에 일을 해줌으로써 자발적 생성 반응을 일으킴
2. 평형의 설명
- 완전 기체 평형
A와 B가 완전 기체일 때는 $\mu=\mu^{\theta}+RTlnp$를 이용하여 반응 Gibbs 에너지를 쓸 수 있음
* 이때 $p=p/p^{\theta}$
$\Delta_r G=\mu_B-\mu_A=(\mu_B^{\theta}+RTlnp_B)-(\mu_A^{\theta}+RTlnp_A)=\Delta_r G^{\theta} +RTln\frac{p_B}{p_A}$
이때 부분 압력들의 비를 Q로 나타내면
$\Delta_r G=\Delta_r G^{\theta}+RTlnQ$ $Q=\frac{p_B}{p_A}$
이때 $\Delta_r G^{\theta}$는 순수한 A,B의 Gibbs 에너지 차이를, $RTlnQ$는 두 물질이 섞일 때 반응이 진행되는 정도를 나타냄
* $\Delta_r G^{\theta}=G_m^{\theta}(B)-G_m^{\theta}(A)=\mu_B^{\theta}-\mu_A^{\theta}$로 반응물과 생성물의 표준 몰 Gibbs 에너지 차이를 말함
* 표준 반응 Gibbs 에너지는 표준 생성 에너지를 이용해서 나타내기도 함 $\Delta_r G^{\theta}=\Delta_f G^{\theta}(B)-\Delta_f G^{\theta}(A)$
이때 평형에서 $\Delta_r G=0$이고 평형에서의 부분 압력들의 비는 K로 나타냄
$0=\Delta_r G^{\theta}+RTlnK$
$RTlnK=-\Delta_r G^{\theta}$ $K=(\frac{p_B}{p_A})_{equil}$
* K가 크다는 것은 $p_B>>p_A$의 뜻으로 정반응이 많이 일어났다는 것임
# 혼합을 고려할 때와 무시할 때의 반응 진척도와 Gibbs 에너지 그래프

$G=H-TS$에서 혼합을 고려하지 않고, 즉 S 엔트로피를 고려하지 않을 때는 H에 따라서 G값이 선형적으로 변함
하지만 혼합을 고려한다면 $\Delta_{mix} G=nRT(x_Alnx_A+x_Blnx_B)$의 기여를 Gibbs 에너지에 포함시켜야 함
그렇기에 위와 같은 그래프가 그려짐
이때도 마찬가지로 극소치에서 평형을 이룸
# 평형일때의 표준 반응 에너지 $\Delta_r G^{\theta}$의 부호
$\Delta_r G^{\theta}>0$일 때는 K<1 이며 $p_B<p_A$가 되어 반응물 A가 우세함을 뜻함
$\Delta_r G^{\theta}<0$일 때는 K>1 이며 $p_B>p_A$가 되어 생성물 B가 우세함을 뜻함
- 일반적 반응의 경우
지금까지는 $A \rightleftharpoons B$의 반응에 대해서만 이야기 했음
이제는 일반적 반응에 이를 확대해 적용할 것임
우선 $2A+B \rightleftharpoons 3C+D$의 일반적인 반응을 다음과 같이 표현할 수 있음
$0=\sum_J v_JJ$
* 이때 $v_J$는 화학종 J의 화학량적 수
$\Delta_r G=\Delta_r G^{\theta}+RTlnQ$ 일반적 반응에서의 반응 Gibbs 에너지
* 일반적 반응에서도 반응 Gibbs 에너지식은 똑같음
* 하지만 이때 $\Delta_r G^{\theta}$와 $RTlnQ$에 해당하는 값이 달라짐
$\Delta_r G^{\theta}=\sum_{products} v\Delta_f G^{\theta}-\sum_{reactatns} v\Delta_f G^{\theta}$ 표준 반응 Gibbs 에너지
이를 간편하게 나타내면 다음과 같음
$\Delta_r G^{\theta}=\sum_J v\Delta_f G^{\theta}(J)$
반응 가중비 Q는 다음과 같은 꼴로 표시됨
$Q=\frac{생성물 활동도}{반응물 활동도}$
여기서 활동도는 각종들의 것을 화학량적 수만큼씩 가중곱을 취한 것으로 곱셈 기호 $\prod$ 를 이용함
$Q= \prod_J a_J^{v_J}$
# 예시
$2A+3B→C+2D$ 반응에서 $Q=\frac{a_Ca_D^2}{a_A^2a_B^3}$
평형에서 G의 기울기는 0이므로 $\Delta_r G=0$ 이때의 활동도가 평형 상수 K임
$K=(\prod_J a_J^{v_J})_{equil}$ 평형 상수의 정의
$\Delta_r G^{\theta}=-RTlnK$ 열역학적 평형 상수
* 열역학적 평형 상수를 이용하면 임의의 반응에 대한 평형 상수를 계산할 수 있고 또한 평형 조성도 예측할 수 있음
- 평형 상수들 사이의 관계
평형 상수를 논할때, 활동도를 그대로 사용하기 보다는 농도와 연관시켜 사용하는 경우가 많음
$a_J=\gamma_Jx_J$, $a_J=\gamma_J b_J/b^{\theta}$, $a_J=[J]/c^{\theta}$를 이용해야 함
* 이때 셋 중 어떤 것을 이용하느냐에 따라 $\gamma_J$값이 달라질 수 있음
* 여기서 $x_J$는 몰분율, $b_J$는 몰랄 농도, [J]는 몰농도임
이때 평형상수를 농도와 연관시키면 다음과 같은 식이 유도됨
$K=K_c \times (\frac{c^{\theta}RT}{p^{\theta}})^{\Delta V}$
이때 괄호 안의 값은 T/(12.03K)가 됨
- 평형 상수의 분자 수준 해석
평형 상수와 Boltzmann 분포 법칙을 연관시켜 이야기할 수 있음
원자들은 두 에너지 준위 세트를 구분하지 않고 모든 준위에 Boltzmann 분포 법칙에 따라 분포되는데, 온도가 주어지면 그 온도에 고유한 개체수 분포가 나타나며 반응 혼합물이 고유한 조성을 가지게 되는 것임

* 이때 두 가지 그림 모두 흡열 반응 $A→B$를 나타낸 것임
첫 번째 그림의 경우 생성물과 반응물의 에너지 준위가 비슷함
G=H-TS 에서 S의 변화가 0이므로 G<0이 되기 위해서 H<0이 되어야 함
두 번째 그림의 경우 B의 에너지 준위 밀도가 A의 에너지 준위 밀도에 비해 매우 큼
A에서 B로 반응할 때 S>0이고 H<0이므로 G<0임
이때 $\Delta_r G^{\theta} =\Delta_r H^{\theta}-T\Delta_r S^{\theta}$ 와 $\Delta_r G^{\theta}=-RTlnK$ 를 이용하면
$K=e^{-\Delta_r H^{\theta}/RT}e^{\Delta_r S^{\theta}/R}$
만약 흡열 반응, 즉 $\Delta_r H^{\theta}>0$이면 $e^{-\Delta_r H^{\theta}/RT}$는 0에 가까워지고 즉 $\Delta_r S^{\theta}$에 의해 K값이 결정 됨
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 6-2 평형에 영향을 주는 요인 (0) | 2024.09.21 |
|---|---|
| 【물리화학1】 6장 화학 평형 (1) | 2024.09.20 |
| 【물리화학1】 5-6 이온의 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-5 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |