0. 이전 이야기
5-2장에서 배웠던 혼합 Gibbs에너지를 통해 5-3장에서는 액체와 기체가 공존할 때 상평형 그림에 대하여 학습하였는데, 이들은 모두 2성분 계였음
5-4장에서는 3성분 계의 상평형 그림에 대하여 학습하였음
3성분 계의 경우 등변 삼각형을 이용하여 상평형 그림을 나타내며, 세 성분들의 몰 분율 합이 1인 것을 이용함
https://nate0707.tistory.com/89
【물리화학1】 5-4 3성분 계의 상평형 그림
0. 이전 이야기 5-3장에서는 액체와 기체가 있을 때의 상평형 그림에 대하여 학습하였음이때 액체와 증기가 공존하는 영역이 존재하는데, 이때의 상대적 양은 지레 규칙을 활용해서 구할 수 있
nate0707.tistory.com
3-4 1법칙과 2법칙의 결합에서는 퓨가시티를 정의하여 진짜 압력 p 대신 유효압력 f를 이용해 이상적 행동으로부터의 이탈을 매우 간단히 처리했음
이와 비슷하게 용액의 경우에도 활동도라는 개념을 이용해 이상 용액에 적용하여 이상적 행동으로부터의 이탈을 설명할 것임
https://nate0707.tistory.com/81
【물리화학1】 3-4 1법칙과 2법칙의 결합
0. 이전이야기 엔트로피를 이용하여 자발성을 따질 경우 계와 주위의 엔트로피를 모두 조사하여야 함따라서 이를 간편화하기 위해 계만을 조사해서 자발성을 따질 수 있는 Helmholtz 에너지와 Gibb
nate0707.tistory.com
1. 용매의 활동도
- 활동도의 정의
실제 용액과 이상 용매에 적용되는 화학 퍼텐셜 일반식은 다음과 같음
$\mu_A=\mu_A^*+RTln(p_A/p_A^*)$
이상 용액의 경우 전체 농도 범위에서 용매가 Raoult의 법칙을 만족 시킴
* $p_A=x_Ap_A^*$
즉 $\mu_A=\mu_A^*+RTlnx_A$
이때 실제 용액의 경우 Raoult의 법칙을 만족시키지 않으므로 다음과 같이 활동도 $a_A$를 이용함
$\mu_A=\mu_A^*+RTlna_A$ 용매 활동도의 정의
즉, $a_A=\frac{p_A}{p_a^*}$
- 활동도 계수
이러한 활동도는 활동도 계수 $\gamma$를 이용해 나타낼 수 있음
$a_A=\gamma_Ax_A$ 이때 $x_A→1$일 때 $\gamma_A→1$로 가서 $a_A=x_A$에 수렴함
이러한 활동도를 이용하면 용매의 화확 퍼텐셜을 다음과 같이 나타낼 수 있음
$\mu_A=\mu_A^*+RTlnx_A+RTln\gamma_A$
2. 용질의 활동도
용질의 활동도도 용매의 활동도와 매우 유사함
- 이상적 묽은 용액
Henry의 법칙에 따르면 $p_B=K_Bx_B$
즉 이상적 묽은 용액의 용질 B의 화학 퍼텐셜을 다음과 같이 나타낼 수 있음
$\mu_B=\mu_B^*+RTln(p_B/p_B^*)=\mu_B^*+RTln\frac{K_B}{p_B^*}+RTlnx_B$
이때 $\mu_B^*$ $K_B$ $p_B^*$ 모두 고유한 상수 이므로 위 식의 첫째항과 둘째항을 묶어 하나의 새로운 표준 화학 퍼텐셜로 나타낼 수 있음
$\mu_B^*+RTln\frac{K_B}{p_B^*}=\mu_B^{\theta}$
즉 이를 정리하면
$\mu_B^{\theta}=\mu_B^*+RTln\frac{K_B}{p_B^*}$
$\mu_B=\mu_B^{\theta}+RTlnx_B$
- 실제 용질
이상적 묽은 용액으로부터 벗어나는 실제의 경우 $x_B$ 대신에 활동도 $a_B$를 넣어서 나타냄
$\mu_B=\mu_B^{\theta}+RTlna_B$ 용질 활동도의 정의
이를 위의 용매 활동도 측정과 같은 방법으로 계산하면
$a_B=\frac{p_B}{K_B}$ 용질 활동도의 측정
활동도 계수 $\gamma_B$를 이용하면 다음과 같음
$a_B=\gamma_Bx_B$ 용질의 활동도 계수 정의
$x_B→0$일때, $a_B→x_B$이고 $\gamma_B→1$임
이를 정리하면
$\mu_B=\mu_B^{\theta}+RTlnx_B$
대신 이때의 $\mu_B^{\theta}$와 용질을 구할때 $\mu_B^{\theta}$와는 값이 다름
- 몰랄농도에 입각한 활동도
$n_B<<n_A$, $n_B \approx \frac{n_B}{n_A}$임을 이용하면
$b_B=\frac{n_B}{1kg of A}=\frac{n_B}{M} \frac{1kg of A}{M}=\frac{n_B}{Mn_A}=\frac{x_B}{M}$
즉 $x_B \approx M_Ab_B$
$\mu_B(l)=\mu_B^*(l)+RTlnb_BM_A=\mu_B^*(l)+RTlnb_BM_A \frac{b^{\theta}}{b^{\theta}}=\mu_B^*(l)+RTlnb^{\theta}M_A+RTln\frac{b_B}{b^{\theta}}$
이때 $\mu_B^*(l)+RTlnb^{\theta}M_A$가 일정하므로
$\mu_B(l)=\mu_B^{\theta}+RTln\frac{b_B}{b^{\theta}}$
만약 실제 용액이라면
$a_B=\gamma_B \frac{b_B}{b^{\theta}}$이고
$\mu_B=\mu_B^{\theta}+RTlna_B=\mu_B^{\theta}+RTln\frac{b_B}{b^{\theta}}+RTln\gamma_B$
- 생화학적 표준 상태
수소 이온의 규약상의 표준 상태는 정상적인 생화학적 조건에 적합하지 않음
* 단위 활동도로서 pH=0이므로
따라서 pH=7로 놓는 생화학적 표준 상태를 사용함
$\mu_{H^+}=\mu_{H^+}^{\ominus}+RTlna_{H^+}=\mu_{H^+}^{\ominus}-(RTln10)pH$
즉, $\mu_{H^+}^{ \oplus }=\mu_{H^+}^{ \ominus }-7RTln10$
3. 정규 용액의 활동도
- 정규 용액이란
정규용액은 AA,BB,AB 상호작용만 고려하고 분자의 clustering을 무시함
$H^E≠0$, $S^E=0$
$H^E=n \xi RTx_Ax_B$
$\xi>0$일 경우 A-B 상호작용이 더 약해 혼합이 흡열 반응을 일으킴
* $\xi>0$일 경우 Gibbs 에너지 변화가 덜 줄어들게 되는데, 이는 덜 자발적인 것을 의미함
$\xi<0$일 경우 A-B 상호작용이 더 강해 혼합이 발열 반응을 일으킴
* $\xi<0$일 경우 Gibbs 에너지 변화가 더 크게 감소하는데, 이는 더 자발적인 것을 의미함
- 정규 용액의 활동도
정규 용액에 대한 활동도의 식은 다음과 같음
$ln \gamma_A=\xi x_B^2$ $ln \gamma_B=\xi x_A^2$ Margules 식
이 식을 이용하여 활동도를 나타내면 다음과 같음
$a_A=\gamma_Ax_A=x_Ae^{\xi x_B^2}=x_Ae^{\xi(1-x_A)^2}$
한편 A의 활동도 $a_A=p_A/p_A^*$이므로
$p_A=p_A^*x_Ae^{\xi(1-x_A)^2}$
이를 만족하는 그래프는 다음과 같음
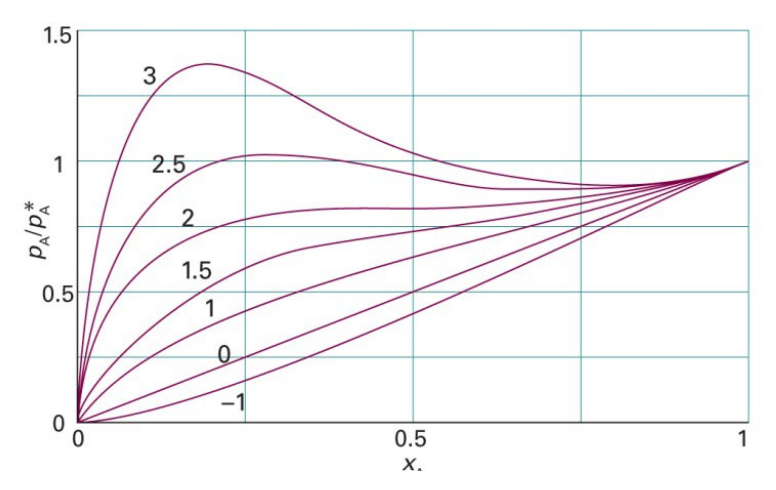
$\xi=0$일 때, $p_A=p_A^*x_A$이며 Raoult의 법칙을 만족함
$\xi>0$일 때, $G^E>0$으로 이상보다 실제의 Gibbs 에너지가 증가하므로 AA,BB 상호작용을 선호하고 A-B 섞이기는 싫어함
흡열 혼합이며 쉽게 기화하므로 증기 압력이 높음
$\xi<0$일 때, $G^E<0$으로 이상보다 실제의 Gibbs 에너지가 감소하므로 A-B 상호작용을 선호함, 발열 반응이고 기화가 어렵기 때문에 증기 압력이 낮음
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 6장 화학 평형 (1) | 2024.09.20 |
|---|---|
| 【물리화학1】 5-6 이온의 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-3 2성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-2 용액의 성질 (4) | 2024.09.17 |
0. 이전 이야기
5-2장에서 배웠던 혼합 Gibbs에너지를 통해 5-3장에서는 액체와 기체가 공존할 때 상평형 그림에 대하여 학습하였는데, 이들은 모두 2성분 계였음
5-4장에서는 3성분 계의 상평형 그림에 대하여 학습하였음
3성분 계의 경우 등변 삼각형을 이용하여 상평형 그림을 나타내며, 세 성분들의 몰 분율 합이 1인 것을 이용함
https://nate0707.tistory.com/89
【물리화학1】 5-4 3성분 계의 상평형 그림
0. 이전 이야기 5-3장에서는 액체와 기체가 있을 때의 상평형 그림에 대하여 학습하였음이때 액체와 증기가 공존하는 영역이 존재하는데, 이때의 상대적 양은 지레 규칙을 활용해서 구할 수 있
nate0707.tistory.com
3-4 1법칙과 2법칙의 결합에서는 퓨가시티를 정의하여 진짜 압력 p 대신 유효압력 f를 이용해 이상적 행동으로부터의 이탈을 매우 간단히 처리했음
이와 비슷하게 용액의 경우에도 활동도라는 개념을 이용해 이상 용액에 적용하여 이상적 행동으로부터의 이탈을 설명할 것임
https://nate0707.tistory.com/81
【물리화학1】 3-4 1법칙과 2법칙의 결합
0. 이전이야기 엔트로피를 이용하여 자발성을 따질 경우 계와 주위의 엔트로피를 모두 조사하여야 함따라서 이를 간편화하기 위해 계만을 조사해서 자발성을 따질 수 있는 Helmholtz 에너지와 Gibb
nate0707.tistory.com
1. 용매의 활동도
- 활동도의 정의
실제 용액과 이상 용매에 적용되는 화학 퍼텐셜 일반식은 다음과 같음
이상 용액의 경우 전체 농도 범위에서 용매가 Raoult의 법칙을 만족 시킴
*
즉
이때 실제 용액의 경우 Raoult의 법칙을 만족시키지 않으므로 다음과 같이 활동도 를 이용함
용매 활동도의 정의
즉,
- 활동도 계수
이러한 활동도는 활동도 계수 를 이용해 나타낼 수 있음
이때 일 때 로 가서 에 수렴함
이러한 활동도를 이용하면 용매의 화확 퍼텐셜을 다음과 같이 나타낼 수 있음
2. 용질의 활동도
용질의 활동도도 용매의 활동도와 매우 유사함
- 이상적 묽은 용액
Henry의 법칙에 따르면
즉 이상적 묽은 용액의 용질 B의 화학 퍼텐셜을 다음과 같이 나타낼 수 있음
이때 모두 고유한 상수 이므로 위 식의 첫째항과 둘째항을 묶어 하나의 새로운 표준 화학 퍼텐셜로 나타낼 수 있음
즉 이를 정리하면
- 실제 용질
이상적 묽은 용액으로부터 벗어나는 실제의 경우 대신에 활동도 를 넣어서 나타냄
용질 활동도의 정의
이를 위의 용매 활동도 측정과 같은 방법으로 계산하면
용질 활동도의 측정
활동도 계수 를 이용하면 다음과 같음
용질의 활동도 계수 정의
일때, 이고 임
이를 정리하면
대신 이때의 와 용질을 구할때 와는 값이 다름
- 몰랄농도에 입각한 활동도
, 임을 이용하면
즉
이때 가 일정하므로
만약 실제 용액이라면
이고
- 생화학적 표준 상태
수소 이온의 규약상의 표준 상태는 정상적인 생화학적 조건에 적합하지 않음
* 단위 활동도로서 pH=0이므로
따라서 pH=7로 놓는 생화학적 표준 상태를 사용함
즉,
3. 정규 용액의 활동도
- 정규 용액이란
정규용액은 AA,BB,AB 상호작용만 고려하고 분자의 clustering을 무시함
,
일 경우 A-B 상호작용이 더 약해 혼합이 흡열 반응을 일으킴
* 일 경우 Gibbs 에너지 변화가 덜 줄어들게 되는데, 이는 덜 자발적인 것을 의미함
일 경우 A-B 상호작용이 더 강해 혼합이 발열 반응을 일으킴
* 일 경우 Gibbs 에너지 변화가 더 크게 감소하는데, 이는 더 자발적인 것을 의미함
- 정규 용액의 활동도
정규 용액에 대한 활동도의 식은 다음과 같음
Margules 식
이 식을 이용하여 활동도를 나타내면 다음과 같음
한편 A의 활동도 이므로
이를 만족하는 그래프는 다음과 같음

일 때, 이며 Raoult의 법칙을 만족함
일 때, 으로 이상보다 실제의 Gibbs 에너지가 증가하므로 AA,BB 상호작용을 선호하고 A-B 섞이기는 싫어함
흡열 혼합이며 쉽게 기화하므로 증기 압력이 높음
일 때, 으로 이상보다 실제의 Gibbs 에너지가 감소하므로 A-B 상호작용을 선호함, 발열 반응이고 기화가 어렵기 때문에 증기 압력이 낮음
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 6장 화학 평형 | 2024.09.20 |
|---|---|
| 【물리화학1】 5-6 이온의 활동도 | 2024.09.19 |
| 【물리화학1】 5-4 3성분 계의 상평형 그림 | 2024.09.18 |
| 【물리화학1】 5-3 2성분 계의 상평형 그림 | 2024.09.18 |
| 【물리화학1】 5-2 용액의 성질 | 2024.09.17 |