0. 이전 이야기
5-2장에서는 이상 용액이 아닌 정규 용액에 대하여 다루었음
실제 용액은 이상 용액과 달리 AA,AB,BB 상호작용과 Clustering 효과를 갖는데, 정규 용액은 이 중 Clustering 효과를 무시함
즉, $H^E≠0$이고 $S^E=0$
이때 $H^E=n \xi RTx_Ax_B$인데 이때 AA,BB 상호작용에 대한 AB의 상대적 상호작용 에너지인 $\xi$의 크기와 부호에 따라 그래프가 다르게 그려짐
그리고 용액 내에 있는 용질 입자의 본질과 상관 없이 용질의 입자 수에만 의존하는 성질인 총괄성에 대해 배움
끓는점 오름, 어는점 내림, 용해도, 삼투에 대하여 다루는데 이때 평형 상태인 경우 양쪽의 화학 퍼텐셜이 같음을 이용함
https://nate0707.tistory.com/87
【물리화학1】 5-2 용액의 성질
0. 이전 이야기 5-1 혼합물에 대한 열역학에서는 서로 반응하지 않는 2성분 혼합물에 대하여 학습하였음이때 분몰 부피와 화학 퍼텐셜인 분몰 Gibbs 에너지를 정의하였고 2성분 혼합물에서의 전
nate0707.tistory.com
1. 증기 압력 상평형 그림
두 휘발성 액체로 된 이상 용액의 각 성분의 부분 증기 압력은 Raoult의 법칙에 의해 다음과 같음
$p_A=x_Ap_A^*$ $p_B=x_Bp_B^*$
따라서 혼합물의 전체 증기 압력은 다음과 같음
$p=p_A+p_B=x_Ap_A^*+x_Bp_B^*=x_Ap_A^*+(1-x_A)p_B^*=p_B^*+(p_A^*-p_B^*)x_A$ 전체 증기 압력
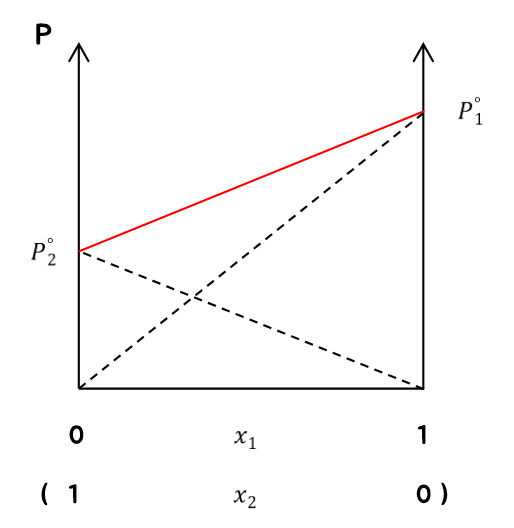
- 증기의 조성
기체 속의 몰분율 $y_A$와 $y_B$는 다음과 같음
$y_A=\frac{p_A}{p}$ $y_B=\frac{p_B}{p}$
즉 증기 압력이 클수록 기체 속의 몰분율도 커짐
혼합물이 이상적이라면 앞서 정리한 전체 증기 압력을 이용해 액체 속의 몰분율을 통해 기체 속의 몰분율을 정리할 수 있음
$y_A=\frac{x_Ap_A^*}{p_B^*+(p_A^*-p_B^*)x_A}$ $y_B=1-y_A$ 증기와 조성
다음 그림은 $p_A^*/p_B^*>1$인 여러 값에서 증기의 조성과 액체 조성을 축으로 나타낸 그림임
A가 B보다 더 휘발성이 좋으므로 항상 $y_A>x_A$를 만족함
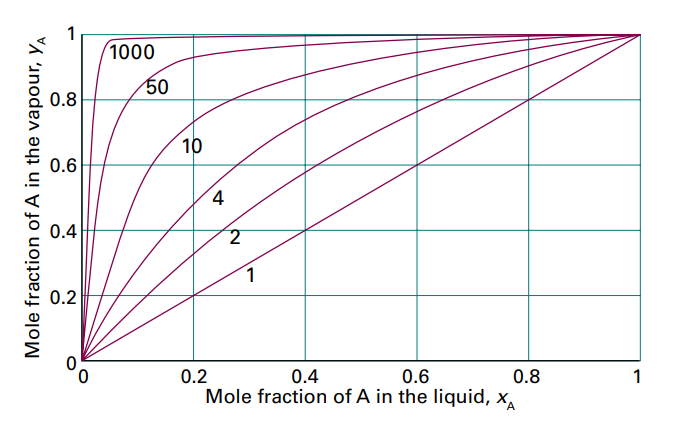
또한 이처럼 전체 증기 압력을 그 증기 자신의 조성만으로도 표현할 수 있음
$p=\frac{p_A^*p_B^*}{p_A^*+(p_B^*-p_A^*)y_A}$
- 상평형 그림의 해석
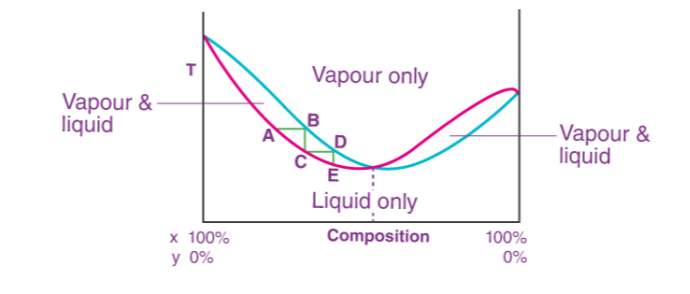
2성분계 상평형 그림은 다음과 같음

이때 두 선으로 둘러싸인 영역 안에서는 액체와 증기가 공존함
여기서 x축과 수평인 선을 하나 그어서 두 선과 만나는 점을 각각 a와 b라고 한다면
a는 조성이 $x_A$인 용액의 증기 압력을 나타내며, b는 이 증기 압력에서 액체와 평형을 이루고 있는 증기의 조성을 나타냄
이때 a-b를 연결하는 선을 맺음선, 이와 수직이 되는 선을 등조성선이라고 부름
- 지레 규칙
평형을 이루고 있는 두상의 상대적 양을 구하려면 맺음선 상의 거리를 측정하고 지레 규칙을 적용시키면 됨
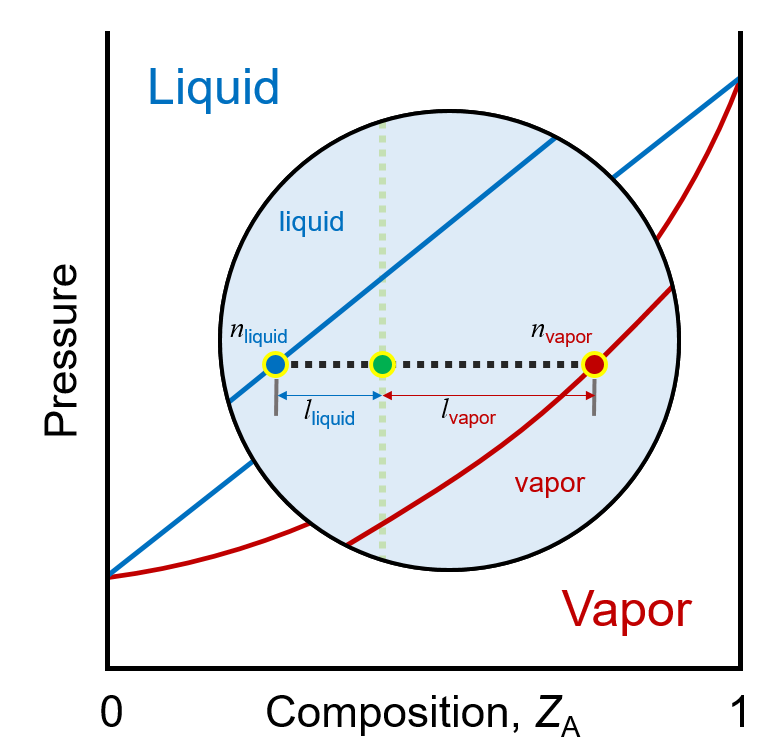
$n_al_a=n_bl_b$ 지레 규칙
2. 온도-조성 상평형 그림
- 혼합물의 증류
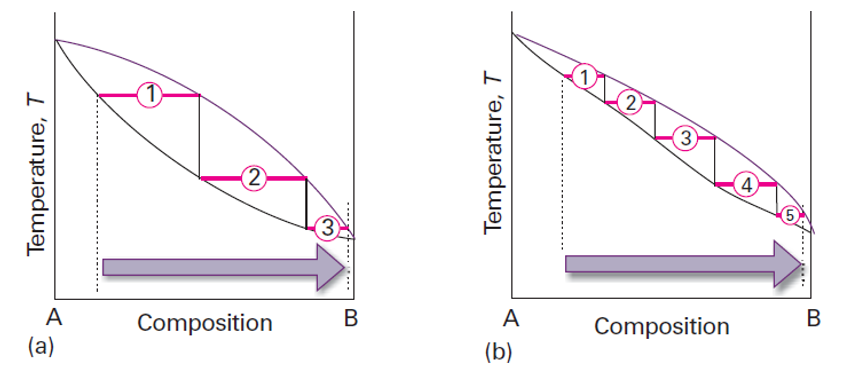
다음 그림은 증류를 설명하기 위한 온도-조성 상평형 그림임
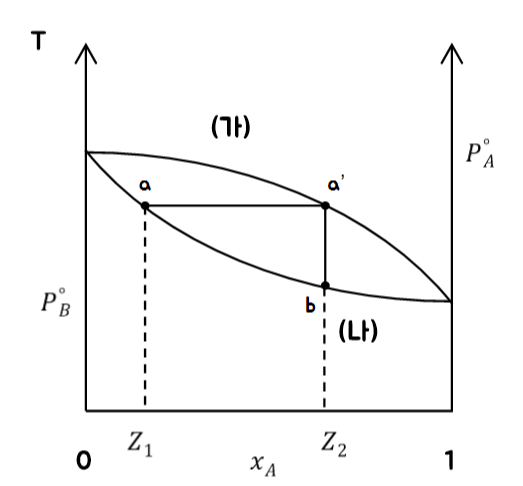
단순 증류는 증기를 뽑아내서 응축
분별 증류는 이러한 끓고 응축되는 과정을 연달아 하는 것을 말함
여기서 특정 a0를 가열해 온도 T1인 a가 되었음
이때 끓는점인 a에서 액체의 조성은 a가 되며 증기의 조성은 a'이 됨
분별 증류관의 효율은 주어진 증류물로부터 주어진 조성의 응축물을 얻는데 필요한 증발과 응축의 유효 단계수인 이론단의 수를 가지고 나타냄
- 불변 끓음 혼합물
불변 끓은 혼합물(azeotrope)이란 혼합물이지만 그 끓는점이 하나로 일정한 혼합물을 말함
이상성으로부터 현저히 벗어나게 행동하는 액체들도 많은데, 이때 A-B 상호작용이 주된 문제가 됨
아래의 그림은 A-B 상호작용보다 AA,BB 각각 있는 것을 선호함, 즉 혼합물이 이상적인 경우보다 안정하지 못함
이러한 경우 계의 $G^E$가 양이며 끓는점이 낮아짐
- 혼합되지 않는 액체
옥탄과 물 같이 서로 섞이지 않는 액체들도 존재함
이들의 혼합물의 전체 증기 압력은 $p=p_A^*+p_B^*$
이 증기 압력이 대기 압력과 같아질 때까지 온도를 높여주면 끓기 시작함
수증기 증류 : 끓는점이 높고, 물에 거의 녹지 않는 유기화합물에 수증기를 불어넣어, 그 물질의 끓는점보다 낮은 온도에서 수증기와 함께 유출되어 나오는 물질의 증기를 냉각하여, 물과의 혼합물로서 응축시키고 그것을 분리시키는 증류법
3. 액체-액체 상평형 그림
- 상 분리
모든 온도에서 어떠한 비율로나 섞이지 않고, 부분족으로 섞이는 액체 쌍 계가 존재함
특정 온도 구간에서 계가 두 상을 가지게 되는데, 하나는 B로 포화된 A 다른 하나는 A로 포화된 B임
두 상의 상대적 존재량은 지레 규칙으로 계산 가능함
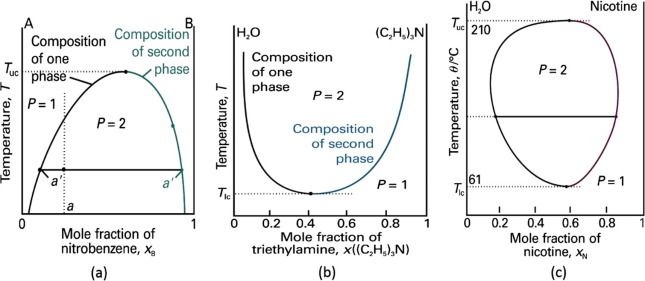
- 임계 용해 온도
위 임계 용해 온도 $T_{uc}$는 상 분리가 일어날 수 있는 온도의 상한을 말함
임계 용해 온도를 기준으로 2개의 상이 존재하는 것을 알 수 있음
임계 용해 온도의 열역학적 고찰은 5-2장에서 배운 혼합 Gibbs 에너지를 이용해야 함
어떤 계는 아래 임계 용해 온도 $T_{ic}$를 갖고 있기도 함, 이는 이보다 낮은 온도에서 섞이고 높은 온도에서는 두 상을 이룸
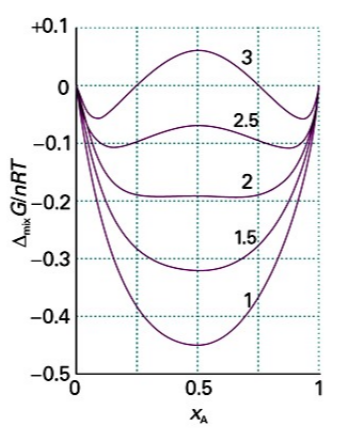
$H^E=\xi RTx_Ax_B$인데, 여기서 $\xi>2$일 경우 혼합 Gibbs 에너지는 두 극소점을 나타냄
따라서 $\partial \Delta_{mix} G/ \partial x=0$이 되는 조건을 찾으면 극소점에 해당하는 조성을 구할 수 있음
이를 계산하면
$ln\frac{x_A}{1-x_A}=-\xi (1-2x_A)$에서의 교점을 구하면 됨
이때 $\xi$값이 크다 = A-B상호작용 작다 =AA,BB따로 있고 싶다 인데,
$\xi$값이 클 수록 교차점이 가운데를 기준으로 멀어져 각각의 순수한 물질로 이동함
- 부분적으로 혼합되는 액체
서로 부분적으로 섞이며 낮은 불변 끓음 혼합물을 형성하는 액체를 가정했을때, 이들은 두 종류의 분자가 서로를 멀리하는 경향을 나타냄
* 그러므로 낮은 끓는점에도 증기로 변함
이때 두 액체가 끓기 전에는 완전히 혼합되는 경우와 완전 혼합이 일어나기 전에 끓게 되는 경우가 있음
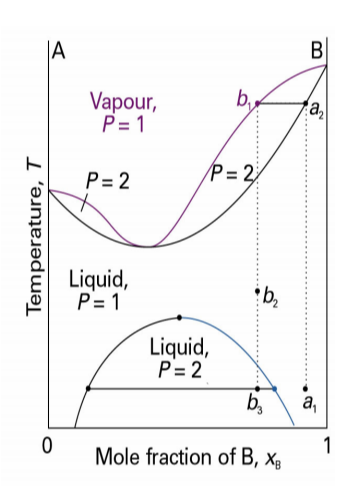

4. 액체-고체 상평형 그림
- 공융 혼합물
공융 혼합물이란 둘 이상의 고체 상태와 하나의 액체 상태로 구성된 계를 말함
즉 액체에서 동시에 정출되는 2종 이상의 결정 혼합물
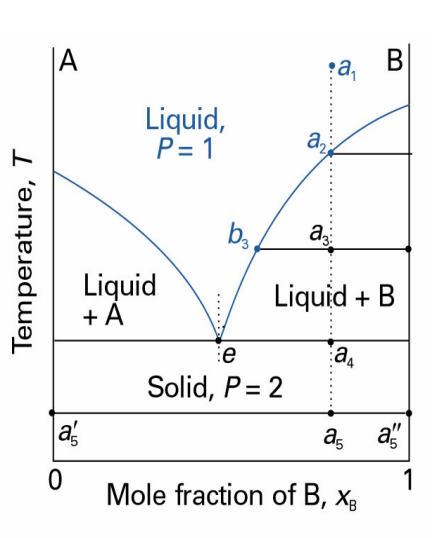
이때 e~a4까지의 구간을 기르면 다음과 같음
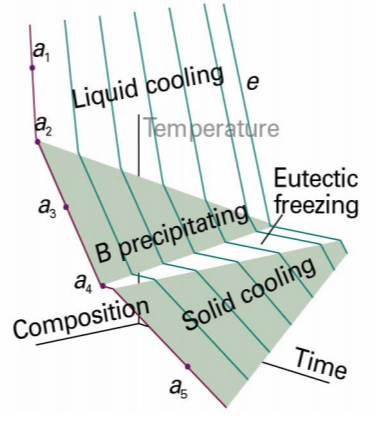
공융 멈춤 :액체+B의 상태에서 냉각이 이어지다가 남아 있는 액체의 조성이 공융 조성e에 도달하면 전체 시료가 고체화 될 때까지 온도가 일정하게 유지됨
- 반응계
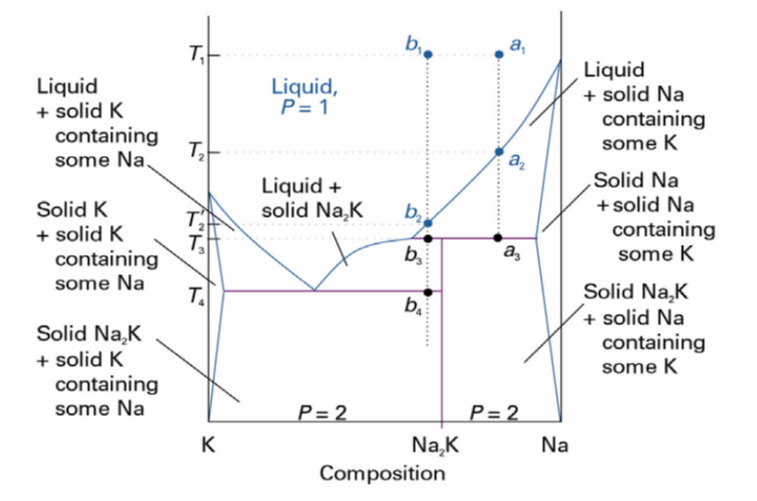
$A+B→C$를 형성하는 계의 상평형 그림은 다음과 같음
과량의 B에 A를 섞어준 계는 C와 미반응 B로 이루어짐
이 계는 C와 B로 된 2성분 계로서 공용 혼합물을 만들 수 있음
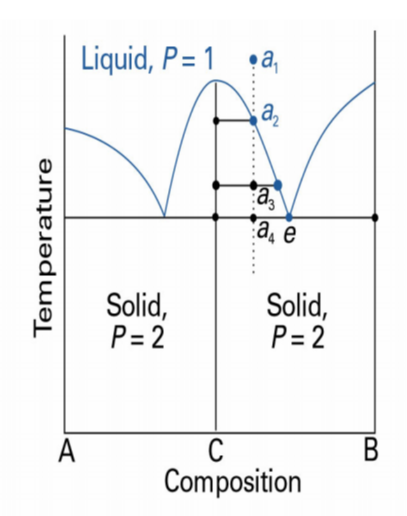
순수한 화합물 C가 녹았을 때, 동일한 조성의 액체로 되는 경우를 합치 녹음이라고 함
액체에서 안정한 것들은 합치녹음을 함
- 비합치 녹음
화합물 C가 액체로서 불안정할 때는 비합치 녹음을 함
이들은 순수한 화합물 C가 녹았을 때 자신의 액체상을 만들지 못하고 성분들로 분해됨
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5-5 활동도 (0) | 2024.09.19 |
|---|---|
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-2 용액의 성질 (4) | 2024.09.17 |
| 【물리화학1】 5-1 혼합물에 대한 열역학 (0) | 2024.09.17 |
| 【물리화학1】 5장 단순 혼합물 (0) | 2024.09.15 |
0. 이전 이야기
5-2장에서는 이상 용액이 아닌 정규 용액에 대하여 다루었음
실제 용액은 이상 용액과 달리 AA,AB,BB 상호작용과 Clustering 효과를 갖는데, 정규 용액은 이 중 Clustering 효과를 무시함
즉, $H^E≠0$이고 $S^E=0$
이때 $H^E=n \xi RTx_Ax_B$인데 이때 AA,BB 상호작용에 대한 AB의 상대적 상호작용 에너지인 $\xi$의 크기와 부호에 따라 그래프가 다르게 그려짐
그리고 용액 내에 있는 용질 입자의 본질과 상관 없이 용질의 입자 수에만 의존하는 성질인 총괄성에 대해 배움
끓는점 오름, 어는점 내림, 용해도, 삼투에 대하여 다루는데 이때 평형 상태인 경우 양쪽의 화학 퍼텐셜이 같음을 이용함
https://nate0707.tistory.com/87
【물리화학1】 5-2 용액의 성질
0. 이전 이야기 5-1 혼합물에 대한 열역학에서는 서로 반응하지 않는 2성분 혼합물에 대하여 학습하였음이때 분몰 부피와 화학 퍼텐셜인 분몰 Gibbs 에너지를 정의하였고 2성분 혼합물에서의 전
nate0707.tistory.com
1. 증기 압력 상평형 그림
두 휘발성 액체로 된 이상 용액의 각 성분의 부분 증기 압력은 Raoult의 법칙에 의해 다음과 같음
$p_A=x_Ap_A^*$ $p_B=x_Bp_B^*$
따라서 혼합물의 전체 증기 압력은 다음과 같음
$p=p_A+p_B=x_Ap_A^*+x_Bp_B^*=x_Ap_A^*+(1-x_A)p_B^*=p_B^*+(p_A^*-p_B^*)x_A$ 전체 증기 압력

- 증기의 조성
기체 속의 몰분율 $y_A$와 $y_B$는 다음과 같음
$y_A=\frac{p_A}{p}$ $y_B=\frac{p_B}{p}$
즉 증기 압력이 클수록 기체 속의 몰분율도 커짐
혼합물이 이상적이라면 앞서 정리한 전체 증기 압력을 이용해 액체 속의 몰분율을 통해 기체 속의 몰분율을 정리할 수 있음
$y_A=\frac{x_Ap_A^*}{p_B^*+(p_A^*-p_B^*)x_A}$ $y_B=1-y_A$ 증기와 조성
다음 그림은 $p_A^*/p_B^*>1$인 여러 값에서 증기의 조성과 액체 조성을 축으로 나타낸 그림임
A가 B보다 더 휘발성이 좋으므로 항상 $y_A>x_A$를 만족함

또한 이처럼 전체 증기 압력을 그 증기 자신의 조성만으로도 표현할 수 있음
$p=\frac{p_A^*p_B^*}{p_A^*+(p_B^*-p_A^*)y_A}$
- 상평형 그림의 해석
2성분계 상평형 그림은 다음과 같음

이때 두 선으로 둘러싸인 영역 안에서는 액체와 증기가 공존함
여기서 x축과 수평인 선을 하나 그어서 두 선과 만나는 점을 각각 a와 b라고 한다면
a는 조성이 $x_A$인 용액의 증기 압력을 나타내며, b는 이 증기 압력에서 액체와 평형을 이루고 있는 증기의 조성을 나타냄
이때 a-b를 연결하는 선을 맺음선, 이와 수직이 되는 선을 등조성선이라고 부름
- 지레 규칙
평형을 이루고 있는 두상의 상대적 양을 구하려면 맺음선 상의 거리를 측정하고 지레 규칙을 적용시키면 됨

$n_al_a=n_bl_b$ 지레 규칙
2. 온도-조성 상평형 그림
- 혼합물의 증류
다음 그림은 증류를 설명하기 위한 온도-조성 상평형 그림임

단순 증류는 증기를 뽑아내서 응축
분별 증류는 이러한 끓고 응축되는 과정을 연달아 하는 것을 말함
여기서 특정 a0를 가열해 온도 T1인 a가 되었음
이때 끓는점인 a에서 액체의 조성은 a가 되며 증기의 조성은 a'이 됨
분별 증류관의 효율은 주어진 증류물로부터 주어진 조성의 응축물을 얻는데 필요한 증발과 응축의 유효 단계수인 이론단의 수를 가지고 나타냄

- 불변 끓음 혼합물
불변 끓은 혼합물(azeotrope)이란 혼합물이지만 그 끓는점이 하나로 일정한 혼합물을 말함
이상성으로부터 현저히 벗어나게 행동하는 액체들도 많은데, 이때 A-B 상호작용이 주된 문제가 됨
아래의 그림은 A-B 상호작용보다 AA,BB 각각 있는 것을 선호함, 즉 혼합물이 이상적인 경우보다 안정하지 못함
이러한 경우 계의 $G^E$가 양이며 끓는점이 낮아짐

- 혼합되지 않는 액체
옥탄과 물 같이 서로 섞이지 않는 액체들도 존재함
이들의 혼합물의 전체 증기 압력은 $p=p_A^*+p_B^*$
이 증기 압력이 대기 압력과 같아질 때까지 온도를 높여주면 끓기 시작함
수증기 증류 : 끓는점이 높고, 물에 거의 녹지 않는 유기화합물에 수증기를 불어넣어, 그 물질의 끓는점보다 낮은 온도에서 수증기와 함께 유출되어 나오는 물질의 증기를 냉각하여, 물과의 혼합물로서 응축시키고 그것을 분리시키는 증류법
3. 액체-액체 상평형 그림
- 상 분리
모든 온도에서 어떠한 비율로나 섞이지 않고, 부분족으로 섞이는 액체 쌍 계가 존재함
특정 온도 구간에서 계가 두 상을 가지게 되는데, 하나는 B로 포화된 A 다른 하나는 A로 포화된 B임
두 상의 상대적 존재량은 지레 규칙으로 계산 가능함

- 임계 용해 온도
위 임계 용해 온도 $T_{uc}$는 상 분리가 일어날 수 있는 온도의 상한을 말함
임계 용해 온도를 기준으로 2개의 상이 존재하는 것을 알 수 있음
임계 용해 온도의 열역학적 고찰은 5-2장에서 배운 혼합 Gibbs 에너지를 이용해야 함
어떤 계는 아래 임계 용해 온도 $T_{ic}$를 갖고 있기도 함, 이는 이보다 낮은 온도에서 섞이고 높은 온도에서는 두 상을 이룸

$H^E=\xi RTx_Ax_B$인데, 여기서 $\xi>2$일 경우 혼합 Gibbs 에너지는 두 극소점을 나타냄
따라서 $\partial \Delta_{mix} G/ \partial x=0$이 되는 조건을 찾으면 극소점에 해당하는 조성을 구할 수 있음
이를 계산하면
$ln\frac{x_A}{1-x_A}=-\xi (1-2x_A)$에서의 교점을 구하면 됨
이때 $\xi$값이 크다 = A-B상호작용 작다 =AA,BB따로 있고 싶다 인데,
$\xi$값이 클 수록 교차점이 가운데를 기준으로 멀어져 각각의 순수한 물질로 이동함
- 부분적으로 혼합되는 액체
서로 부분적으로 섞이며 낮은 불변 끓음 혼합물을 형성하는 액체를 가정했을때, 이들은 두 종류의 분자가 서로를 멀리하는 경향을 나타냄
* 그러므로 낮은 끓는점에도 증기로 변함
이때 두 액체가 끓기 전에는 완전히 혼합되는 경우와 완전 혼합이 일어나기 전에 끓게 되는 경우가 있음


4. 액체-고체 상평형 그림
- 공융 혼합물
공융 혼합물이란 둘 이상의 고체 상태와 하나의 액체 상태로 구성된 계를 말함
즉 액체에서 동시에 정출되는 2종 이상의 결정 혼합물

이때 e~a4까지의 구간을 기르면 다음과 같음

공융 멈춤 :액체+B의 상태에서 냉각이 이어지다가 남아 있는 액체의 조성이 공융 조성e에 도달하면 전체 시료가 고체화 될 때까지 온도가 일정하게 유지됨
- 반응계
$A+B→C$를 형성하는 계의 상평형 그림은 다음과 같음
과량의 B에 A를 섞어준 계는 C와 미반응 B로 이루어짐
이 계는 C와 B로 된 2성분 계로서 공용 혼합물을 만들 수 있음

순수한 화합물 C가 녹았을 때, 동일한 조성의 액체로 되는 경우를 합치 녹음이라고 함
액체에서 안정한 것들은 합치녹음을 함
- 비합치 녹음
화합물 C가 액체로서 불안정할 때는 비합치 녹음을 함
이들은 순수한 화합물 C가 녹았을 때 자신의 액체상을 만들지 못하고 성분들로 분해됨

'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5-5 활동도 (0) | 2024.09.19 |
|---|---|
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-2 용액의 성질 (4) | 2024.09.17 |
| 【물리화학1】 5-1 혼합물에 대한 열역학 (0) | 2024.09.17 |
| 【물리화학1】 5장 단순 혼합물 (0) | 2024.09.15 |