0. 이전 이야기
5-1 혼합물에 대한 열역학에서는 서로 반응하지 않는 2성분 혼합물에 대하여 학습하였음
이때 분몰 부피와 화학 퍼텐셜인 분몰 Gibbs 에너지를 정의하였고 2성분 혼합물에서의 전체 Gibbs 에너지를 이용해 Gibbs-Duhem식도 유도하였음
완전 기체 분몰 Gibbs 에너지를 이용해 화학 퍼텐셜을 계산하였고, 이를 이용해 기체의 혼합 전 후의 $\Delta_{mix} G$를 구하였음
이때 $\Delta_{mix} G<0$이므로 완전 기체는 어떤 비율로 있든 자발적으로 섞임
그리고 이러한 Gibbs 에너지를 이용해 완전 기체의 혼합 엔트로피와 혼합 엔탈피를 구하였음
마지막으로 액체의 화학 퍼텐셜에 대하여도 학습하였는데, 이때 평형 상태일 경우 액체와 기체의 화학 퍼텐셜이 같음을 이용함
이를 이용하면 $\mu_A=\mu_A^*+RTln\frac{p_A}{p^*}$를 구할 수 있음
또한 여기서 각 성분의 부분 압력과 순수한 액체의 증기 압력과의 비 $p_A/p_A^*$가 용액 속의 A의 몰분율과 같음
$p_A=x_pp_A^*$ 이를 이상 용액의 Raoult의 법칙이라고 부름
용질의 경우 Raoult의 법칙을 만족하지 않지만, 용질 또한 용질의 증기 압력이 몰 분율에 비례함
이를 이용해 $p_B=x_BK_B$라는 Henry의 법칙을 도출해 냄
https://nate0707.tistory.com/86#-%20%EB%B6%84%EB%AA%B0%20%EB%B6%80%ED%94%BC-1
【물리화학1】 5-1 혼합물에 대한 열역학
0. 이전이야기 4장에서는 순수한 물질의 상평형 그림에 대하여 학습하였고, 화학 퍼텐셜을 이용해 상평형 그림을 설명함하지만 일상에서 더 유용한 부분은 혼합물에 대한 열역학으로 5장에서
nate0707.tistory.com
이상 용액에서의 열역학적 결과는 추후 이상성을 벗어나는 실제 용액을 다루는 기초가 됨
1. 액체 혼합물
이상 용액에서 가장 중요한 개념은 이상 용액의 화학 퍼텐셜임 $\mu_J=\mu_J^*+RTlnx_J$
그리고 이상적 혼합물이나 용액속의 성분의 화학 퍼텐셜은 $/mu_J$ 순수할 때의 값은 $\mu_J^*$로 표기함
- 이상 용액
두 액체가 이상 용액을 만들때 혼합되기 전의 Gibbs 에너지는 다음과 같음
$G_i=n_A\mu_A^*+n_B\mu_B^*$
혼합 후의 Gibbs 에너지는 다음과 같음
$G_f=n_A(\mu_A^*+RTlnx_A)+n_B(\mu_B^*+RTlnx_B)$
따라서 $\Delta_{mix} G=nRT(x_Alnx_A+x_Blnx_B)$ 이상 용액의 혼합 Gibbs 에너지
* 여기서 $n=n_A+n_B$
$\Delta_{mix} S=-nR(x_Alnx_A+x_Blnx_B)$ 이상 용액의 혼합 엔트로피
$\Delta_{mix} H=0$
이는 앞서 5-1 혼합물에 대한 열역학에서 모두 학습하였음
https://nate0707.tistory.com/86
【물리화학1】 5-1 혼합물에 대한 열역학
0. 이전이야기 4장에서는 순수한 물질의 상평형 그림에 대하여 학습하였고, 화학 퍼텐셜을 이용해 상평형 그림을 설명함하지만 일상에서 더 유용한 부분은 혼합물에 대한 열역학으로 5장에서
nate0707.tistory.com
$\Delta_{mix} V=(\partial \Delta_{mix} G/ \partialp)_T=0$
*G는 압력과 무관한 함수이므로
위에서 이상 용액의 혼합 Gibbs 에너지와 혼합 엔트로피는 두 완전 기체가 혼합될 때의 식과 똑같음
하지만 용액의 이상성과 기체의 이상성 사이에는 차이점이 존재함
완전 기체의 경우 분자들 사이에 상호작용이 없지만, 이상 용액에서는 상호작용이 있으며 용액에서의 평균 A-B 상호작용이 두 순수한 액체에서의 평균 A-A 및 B-B 상호작용과 같음
실제 용액의 경우 A-A,A-B,B-B 분자들 사이의 상호작용이 모두 다름
따라서 액체들이 혼합할 때 엔탈피와 부피가 변하기도 하며 엔탈피가 크게 증가하거나 엔트로피가 덜 감소할 때 혼합 Gibbs 에너지가 양이될 수 있음
* $G=H-TS$인데, H가 크거나 엔트로피가 작을 경우 G가 양수가 될 수 있음
이러한 경우 분리 과정이 오히려 자발적으로 일어나거나 한정된 조성 영역에서만 섞이는 부분 혼합이 일어날 수도 있음
- 과잉 함수의 정규 용액
과잉 함수 $X^E$ : 실제의 혼합 열역학적 함수와 이상 용액에 대한 혼합 열역학적 함수의 차이
* 실제와 이상용액의 다른 정도를 나타냄
$X^E=\Delta_{mix}X-\Delta_{mix}X^{ideal}$ 과잉 함수의 정의
과잉 엔트로피는 $S^E=\Delta_{mix} S-\Delta_{mix} S^{ideal}$를 이용해서 구하면 되는데
과잉 엔탈피와 부피의 경우 이상 용액에서의 값이 0이므로 측정치만 구하면 됨
과잉 함수가 0으로부터 이탈하는 정도는 그 용액의 비이상성의 정도를 나타내는데, 이때 정규 용액을 사용함
실제 용액의 경우 A-A,A-B,B-B의 상호작용과 분자의 clustering 두개의 영향을 받을 수 있는데
이때 정규 용액은 분자의 clustering을 무시하는 것임
$H^E≠0$이고 $S^E=0$
이때 $H^E=n \xi RTx_Ax_B$
여기서 $\xi$는 AA와 BB 상호작용에 대한 AB의 상대적인 상호작용 에너지를 나타냄
이때 $\xi$의 크기와 부호에 따른 그래프는 다음과 같음
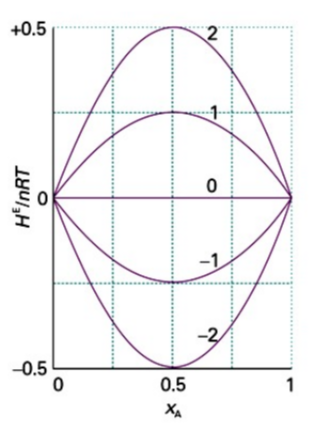
$\xi>0$일 경우 A-B 상호작용이 더 약해 혼합이 흡열 반응을 일으킴
$\xi<0$일 경우 A-B 상호작용이 더 강해 혼합이 발열 반응을 일으킴
$G=H-TS$이므로 정규용액에서 H를 고려한 Gibbs 에너지 변화는 다음과 같음
$\Delta_{mix} G=nRT(x_Alnx_A+x_Blnx_B+\xi x_Ax_B)$

$\xi>2$인 경우에 한 극대치 옆에 2개의 극소치가 나타남, 즉 이 계가 두 극소점에 해당하는 조성의 두 상으로 자발적으로 분리됨
* 분리가 일어남으로써 계의 Gibbs 에너지가 감소함
2. 총괄성
총괄성 : 용액 내에 있는 용질 입자의 본질에는 상관없이 용질 입자의 수에만 의존하는 성질
여기서는 증기 압력 내림, 끓는점 오름, 어는점 내림, 삼투압에 대하여 논의할 것임
이때 주요한 두가지 가정이 있음
첫재 용질은 비휘발성이며 증기에는 아무런 기여를 하지 않음
둘째 용액은 얼 때 순수한 고체 용매가 됨
- 총괄성의 공통 특성
총괄성의 특성은 용매에서 용질이 될때 화학 퍼텐셜이 낮아짐으로써 시작됨
이상 용액의 경우 $\mu_A=\mu_A^*RTlnx_A$인데, $x_A<1$이므로 $lnx_A<0$ 따라서 용질의 화학 퍼텐셜은 순수한 용매보다 낮음
이때 앞서 말한 가정에 의해 용질은 증기나 고체로 변하지 않으므로 이들의 화학 퍼텐셜은 변하지 않음
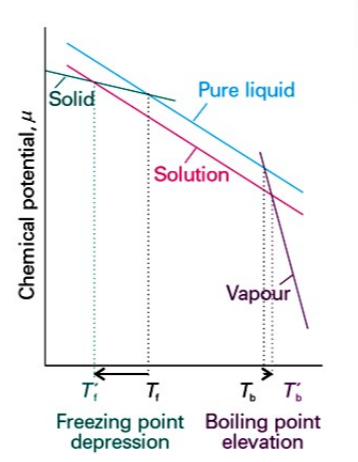
화학 퍼텐셜은 이상 용액의 경우에도 감소함
$\mu=\mu(H,S)$인데, 이상 용액에서 혼합 엔탈피 변화가 0이므로 이는 엔트로피 효과 때문에 발생하는 경우임
용질이 존재할 때는 이상 용액의 경우라도 액체의 엔트로피가 더 커지는데, 용액의 엔트로피는 순수한 액체의 엔트로피보다 높기 때문에 기체가 되려는 경향이 낮아지는 것임
이러한 효과로 증기 압력이 낮아지고 끓는점이 높아짐

마찬가지로 용액에서는 분자들의 무작정성이 증가하기에 얼려는 경향이 억제됨 따라서 고체가 되기위해서는 온도가 더 내려가야 하며 녹는점이 내려가는 것임
- 끓는점 오름
끓는점 오름을 계산할 경우, 용질 B는 기체가 될 수 없으므로 다음과 같은 상태의 평형을 생각해 줘야함
즉 $\mu_A^*(g)=\mu_A^*(l)+RTlnx_A$을 만족하는 온도에서 평형이 이루어짐

용질이 $x_B$의 몰분율로 존재할 때 끓는점이 $T^*$에서 $T^*+\Delta T_b$로 증가하는데 이때 변화량은 다음과 같음
$\Delta T_b=Kx_B$ $K=\frac{R{T*}^2}{\Delta_{vap} H}$ 이상 용액의 끓는점 오름
위의 식은 용질의 종류에는 무관하고 몰분율에만 의존하기에 총괄성을 지님
위 식은 용매의 성질에 의존하는데 3-2장 Trouton 규칙에 의해 $\Delta_{vvap} H/T^*$은 거의 일정하므로 끓는점 오름은 순수한 용매의 끓는점과 비례함
몰분율은 몰랄농도와 비례하므로 다음과 같이 실용적으로 사용하기도 함
$\Delta T_b=K_bb$ 끓는점 오름의 실험적 관계식
* 여기서 $K_b$는 실험적으로 정해서 사용하는 끓는점 오름 상수임
<증명>
$\mu_A^*(g)=\mu_A^*(l)+RTlnx_A$의 식은 다음과 같이 바꿀 수 있음
$lnx_A=\frac{\mu_A^*(g)-\mu_A^*(l)}{RT}=\frac{\Delta_{vap} G}{RT}$
*$\Delta_{vap} G$는 순수한 용매의 증발 Gibbs 에너지
$\frac{dlnx_A}{dT}=\frac{1}{R} \frac{d(\Delta_{vap} G/T)}{dT}=-\frac{\Delta_{vap} H}{RT^2}$
* $(\partial (G/T)/ \partial T)_p=-H/T^2$
양변에 dT를 곱하고 $x_A=1$부터 $x_A$까지 적분하면
$\int_0^{lnx_A} dlnx_A=-\frac{1}{R} \int_{T^*}^T \frac{\Delta_{vap} H}{T^2}dT$
이를 계산하면 $lnx_A=ln(1-x_B)=-\frac{\Delta_{vap} H}{R} \int_{T^*}^T \frac{1}{T^2}dT=\frac{\Delta_{vap} H}{R}(\frac{1}{T}-\frac{1}{T^*})$
용질의 양이 매우 작아서 $x_B<<1$이 된다면 $ln(1-x_B) \approx -x_B$이므로
$x_B=\frac{\Delta_{vap} H}{R}(\frac{1}{T^*}-\frac{1}{T})$
마지막으로 $T \approx T^*$이므로 $\frac{1}{T^*}-\frac{1}{T}=\frac{\Delta T_b}{{T^*}^2}$
- 어는점 내림
어는점 내림은 끓는점 오름에서의 과정과 똑같음
끓는점 오름과 같이, 어는점 내림에서도 두 상 속에 들어있는 물질의 화학 퍼텐셜이 같아야 함
$\mu_A^*(s)=\mu_A^*(l)+RTlnx_A$

따라서 위의 증명을 그대로 유도하면 다음 식이 성립함
$\Delta T_f=K^{'}x_B$ $K^{'}=\frac{R{T*}^2}{\Delta_{fus} H}$ 이상 용액의 어는점 내림
$\Delta T_f=K_fb$ 어는점 내림의 실험적 관계식
* $K_f$는 실험적인 어는점 내림 상수
- 용해도
용해도는 용질의 종류에 따라 변하긴 하지만, 위의 방법과 비슷한 방법으로 용질의 용해도를 구할 수 있음
고체의 용질을 용매에 녹일때, 포화 용액이 될때까지 용질은 녹을 것이고 포화가 될때의 고체 용질의 화학 퍼텐셜과 용액 속의 용질의 화학 퍼텐셜이 같아짐
$\mu_B^*(s)=\mu_B^*(l)+RTlnx_B$
이 식을 위의 증명과정을 거치면
$ln(x_B)=\frac{\Delta_{vap} H}{R} (\frac{1}{T_f}-\frac{1}{T})$
* $\Delta_{fus} H$는 용질의 용융 엔탈피 $T_f$는 녹는점
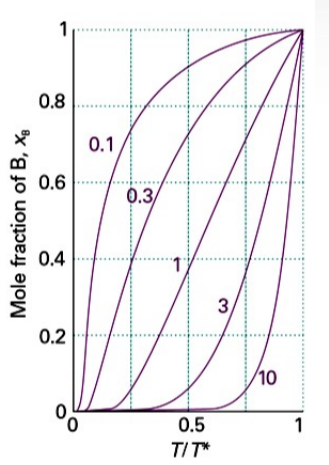
* 각 숫자는 $\Delta_{fus} H/R$값을 나타낸 것
B의 용해도는 온도가 녹는점 $T_f$아래로 내려갈수록 지수함수적으로 감소함
- 삼투
삼투 현상 : 반투과성 막을 경계로 농도가 낮은 용액에서 농도가 높은 용액으로 용매가 이동하는 현상
* 반투막은 용매는 통과시키지만 용질은 통과시키지 못함
삼투압 $\Pi$ : 용매의 유입을 완전히 막기 위해서는 용액에 압력을 가해야 하는데, 이때의 압력을 말함

다음 그림은 용매에 반투과성 막이 있는 용액을 집어넣은 그림임
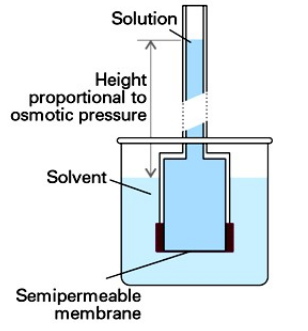
용매가 용액 속으로 흘러들어가 용액 기둥의 수압이 삼투압과 맞먹을때 삼투현상이 멈춤
평형에서는 용매의 화학 퍼텐셜이 반투막의 양 쪽에서 같아야 하는데 이를 이용해 van't Hoff 식을 유도할 수 있음
$\Pi=[B]RT$ van't Hoff 식
* 여기서 $[B]$는 용질의 몰 농도로 $n_B/V$
<증명>
압력이 p인 용매의 화학 퍼텐셜 = 압력이 $p+\Pi$인 용액 속 용매의 화학 퍼텐셜을 보여야 함
$\mu_A(p)^*=\mu_A(x_A,p+\Pi)=\mu_A^*(p+\Pi)+RTlnx_A$
여기서 압력 효과를 이용하기 위해 $G_m(p_f)=G_m(p_i)+\int_{p_i}^{p_f} V_mdp$을 이용하면
$\mu_A^*(p+\Pi)=\mu_A^*(p)+\int_{p}^{p+\Pi} V_mdp$
* 여기서 $V_m$은 순수한 용매 A의 몰 부피
위의 식들을 결합하면 $-RTlnx_A=\int_{p}^{p+\Pi} V_mdp$
$lnx_A=ln(1-x_B) \approx -x_B$이므로
$RTx_B=\Pi V_m$
용액이 묽을 때는 $x_B \approx n_B/n_A$이고 $n_AV_m=V$이므로
$\Pi=\frac{n_b}{V}RT=[B]RT$
고분자의 경우 용해될 때 이상적인 성질을 나타내지 않아 van't Hoff 식을 비리알 전개식을 이용하여 사용함
$\Pi=[B]RT{1+B[J]+...}$ 삼투 비리알 전개식
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
|---|---|
| 【물리화학1】 5-3 2성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-1 혼합물에 대한 열역학 (0) | 2024.09.17 |
| 【물리화학1】 5장 단순 혼합물 (0) | 2024.09.15 |
| 【물리화학1】 4-2 상 전이의 열역학적 양상 (0) | 2024.09.15 |
0. 이전 이야기
5-1 혼합물에 대한 열역학에서는 서로 반응하지 않는 2성분 혼합물에 대하여 학습하였음
이때 분몰 부피와 화학 퍼텐셜인 분몰 Gibbs 에너지를 정의하였고 2성분 혼합물에서의 전체 Gibbs 에너지를 이용해 Gibbs-Duhem식도 유도하였음
완전 기체 분몰 Gibbs 에너지를 이용해 화학 퍼텐셜을 계산하였고, 이를 이용해 기체의 혼합 전 후의 를 구하였음
이때 이므로 완전 기체는 어떤 비율로 있든 자발적으로 섞임
그리고 이러한 Gibbs 에너지를 이용해 완전 기체의 혼합 엔트로피와 혼합 엔탈피를 구하였음
마지막으로 액체의 화학 퍼텐셜에 대하여도 학습하였는데, 이때 평형 상태일 경우 액체와 기체의 화학 퍼텐셜이 같음을 이용함
이를 이용하면 를 구할 수 있음
또한 여기서 각 성분의 부분 압력과 순수한 액체의 증기 압력과의 비 가 용액 속의 A의 몰분율과 같음
이를 이상 용액의 Raoult의 법칙이라고 부름
용질의 경우 Raoult의 법칙을 만족하지 않지만, 용질 또한 용질의 증기 압력이 몰 분율에 비례함
이를 이용해 라는 Henry의 법칙을 도출해 냄
https://nate0707.tistory.com/86#-%20%EB%B6%84%EB%AA%B0%20%EB%B6%80%ED%94%BC-1
【물리화학1】 5-1 혼합물에 대한 열역학
0. 이전이야기 4장에서는 순수한 물질의 상평형 그림에 대하여 학습하였고, 화학 퍼텐셜을 이용해 상평형 그림을 설명함하지만 일상에서 더 유용한 부분은 혼합물에 대한 열역학으로 5장에서
nate0707.tistory.com
이상 용액에서의 열역학적 결과는 추후 이상성을 벗어나는 실제 용액을 다루는 기초가 됨
1. 액체 혼합물
이상 용액에서 가장 중요한 개념은 이상 용액의 화학 퍼텐셜임
그리고 이상적 혼합물이나 용액속의 성분의 화학 퍼텐셜은 순수할 때의 값은 로 표기함
- 이상 용액
두 액체가 이상 용액을 만들때 혼합되기 전의 Gibbs 에너지는 다음과 같음
혼합 후의 Gibbs 에너지는 다음과 같음
따라서 이상 용액의 혼합 Gibbs 에너지
* 여기서
이상 용액의 혼합 엔트로피
이는 앞서 5-1 혼합물에 대한 열역학에서 모두 학습하였음
https://nate0707.tistory.com/86
【물리화학1】 5-1 혼합물에 대한 열역학
0. 이전이야기 4장에서는 순수한 물질의 상평형 그림에 대하여 학습하였고, 화학 퍼텐셜을 이용해 상평형 그림을 설명함하지만 일상에서 더 유용한 부분은 혼합물에 대한 열역학으로 5장에서
nate0707.tistory.com
*G는 압력과 무관한 함수이므로
위에서 이상 용액의 혼합 Gibbs 에너지와 혼합 엔트로피는 두 완전 기체가 혼합될 때의 식과 똑같음
하지만 용액의 이상성과 기체의 이상성 사이에는 차이점이 존재함
완전 기체의 경우 분자들 사이에 상호작용이 없지만, 이상 용액에서는 상호작용이 있으며 용액에서의 평균 A-B 상호작용이 두 순수한 액체에서의 평균 A-A 및 B-B 상호작용과 같음
실제 용액의 경우 A-A,A-B,B-B 분자들 사이의 상호작용이 모두 다름
따라서 액체들이 혼합할 때 엔탈피와 부피가 변하기도 하며 엔탈피가 크게 증가하거나 엔트로피가 덜 감소할 때 혼합 Gibbs 에너지가 양이될 수 있음
* 인데, H가 크거나 엔트로피가 작을 경우 G가 양수가 될 수 있음
이러한 경우 분리 과정이 오히려 자발적으로 일어나거나 한정된 조성 영역에서만 섞이는 부분 혼합이 일어날 수도 있음
- 과잉 함수의 정규 용액
과잉 함수 : 실제의 혼합 열역학적 함수와 이상 용액에 대한 혼합 열역학적 함수의 차이
* 실제와 이상용액의 다른 정도를 나타냄
과잉 함수의 정의
과잉 엔트로피는 를 이용해서 구하면 되는데
과잉 엔탈피와 부피의 경우 이상 용액에서의 값이 0이므로 측정치만 구하면 됨
과잉 함수가 0으로부터 이탈하는 정도는 그 용액의 비이상성의 정도를 나타내는데, 이때 정규 용액을 사용함
실제 용액의 경우 A-A,A-B,B-B의 상호작용과 분자의 clustering 두개의 영향을 받을 수 있는데
이때 정규 용액은 분자의 clustering을 무시하는 것임
이고
이때
여기서 는 AA와 BB 상호작용에 대한 AB의 상대적인 상호작용 에너지를 나타냄
이때 의 크기와 부호에 따른 그래프는 다음과 같음

일 경우 A-B 상호작용이 더 약해 혼합이 흡열 반응을 일으킴
일 경우 A-B 상호작용이 더 강해 혼합이 발열 반응을 일으킴
이므로 정규용액에서 H를 고려한 Gibbs 에너지 변화는 다음과 같음

인 경우에 한 극대치 옆에 2개의 극소치가 나타남, 즉 이 계가 두 극소점에 해당하는 조성의 두 상으로 자발적으로 분리됨
* 분리가 일어남으로써 계의 Gibbs 에너지가 감소함
2. 총괄성
총괄성 : 용액 내에 있는 용질 입자의 본질에는 상관없이 용질 입자의 수에만 의존하는 성질
여기서는 증기 압력 내림, 끓는점 오름, 어는점 내림, 삼투압에 대하여 논의할 것임
이때 주요한 두가지 가정이 있음
첫재 용질은 비휘발성이며 증기에는 아무런 기여를 하지 않음
둘째 용액은 얼 때 순수한 고체 용매가 됨
- 총괄성의 공통 특성
총괄성의 특성은 용매에서 용질이 될때 화학 퍼텐셜이 낮아짐으로써 시작됨
이상 용액의 경우 인데, 이므로 따라서 용질의 화학 퍼텐셜은 순수한 용매보다 낮음
이때 앞서 말한 가정에 의해 용질은 증기나 고체로 변하지 않으므로 이들의 화학 퍼텐셜은 변하지 않음

화학 퍼텐셜은 이상 용액의 경우에도 감소함
인데, 이상 용액에서 혼합 엔탈피 변화가 0이므로 이는 엔트로피 효과 때문에 발생하는 경우임
용질이 존재할 때는 이상 용액의 경우라도 액체의 엔트로피가 더 커지는데, 용액의 엔트로피는 순수한 액체의 엔트로피보다 높기 때문에 기체가 되려는 경향이 낮아지는 것임
이러한 효과로 증기 압력이 낮아지고 끓는점이 높아짐

마찬가지로 용액에서는 분자들의 무작정성이 증가하기에 얼려는 경향이 억제됨 따라서 고체가 되기위해서는 온도가 더 내려가야 하며 녹는점이 내려가는 것임
- 끓는점 오름
끓는점 오름을 계산할 경우, 용질 B는 기체가 될 수 없으므로 다음과 같은 상태의 평형을 생각해 줘야함
즉 을 만족하는 온도에서 평형이 이루어짐

용질이 의 몰분율로 존재할 때 끓는점이 에서 로 증가하는데 이때 변화량은 다음과 같음
이상 용액의 끓는점 오름
위의 식은 용질의 종류에는 무관하고 몰분율에만 의존하기에 총괄성을 지님
위 식은 용매의 성질에 의존하는데 3-2장 Trouton 규칙에 의해 은 거의 일정하므로 끓는점 오름은 순수한 용매의 끓는점과 비례함
몰분율은 몰랄농도와 비례하므로 다음과 같이 실용적으로 사용하기도 함
끓는점 오름의 실험적 관계식
* 여기서 는 실험적으로 정해서 사용하는 끓는점 오름 상수임
<증명>
의 식은 다음과 같이 바꿀 수 있음
*는 순수한 용매의 증발 Gibbs 에너지
*
양변에 dT를 곱하고 부터 까지 적분하면
이를 계산하면
용질의 양이 매우 작아서 이 된다면 이므로
마지막으로 이므로
- 어는점 내림
어는점 내림은 끓는점 오름에서의 과정과 똑같음
끓는점 오름과 같이, 어는점 내림에서도 두 상 속에 들어있는 물질의 화학 퍼텐셜이 같아야 함

따라서 위의 증명을 그대로 유도하면 다음 식이 성립함
이상 용액의 어는점 내림
어는점 내림의 실험적 관계식
* 는 실험적인 어는점 내림 상수
- 용해도
용해도는 용질의 종류에 따라 변하긴 하지만, 위의 방법과 비슷한 방법으로 용질의 용해도를 구할 수 있음
고체의 용질을 용매에 녹일때, 포화 용액이 될때까지 용질은 녹을 것이고 포화가 될때의 고체 용질의 화학 퍼텐셜과 용액 속의 용질의 화학 퍼텐셜이 같아짐
이 식을 위의 증명과정을 거치면
* 는 용질의 용융 엔탈피 는 녹는점

* 각 숫자는 값을 나타낸 것
B의 용해도는 온도가 녹는점 아래로 내려갈수록 지수함수적으로 감소함
- 삼투
삼투 현상 : 반투과성 막을 경계로 농도가 낮은 용액에서 농도가 높은 용액으로 용매가 이동하는 현상
* 반투막은 용매는 통과시키지만 용질은 통과시키지 못함
삼투압 : 용매의 유입을 완전히 막기 위해서는 용액에 압력을 가해야 하는데, 이때의 압력을 말함

다음 그림은 용매에 반투과성 막이 있는 용액을 집어넣은 그림임

용매가 용액 속으로 흘러들어가 용액 기둥의 수압이 삼투압과 맞먹을때 삼투현상이 멈춤
평형에서는 용매의 화학 퍼텐셜이 반투막의 양 쪽에서 같아야 하는데 이를 이용해 van't Hoff 식을 유도할 수 있음
van't Hoff 식
* 여기서 는 용질의 몰 농도로
<증명>
압력이 p인 용매의 화학 퍼텐셜 = 압력이 인 용액 속 용매의 화학 퍼텐셜을 보여야 함
여기서 압력 효과를 이용하기 위해 을 이용하면
* 여기서 은 순수한 용매 A의 몰 부피
위의 식들을 결합하면
이므로
용액이 묽을 때는 이고 이므로
고분자의 경우 용해될 때 이상적인 성질을 나타내지 않아 van't Hoff 식을 비리알 전개식을 이용하여 사용함
삼투 비리알 전개식
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5-4 3성분 계의 상평형 그림 | 2024.09.18 |
|---|---|
| 【물리화학1】 5-3 2성분 계의 상평형 그림 | 2024.09.18 |
| 【물리화학1】 5-1 혼합물에 대한 열역학 | 2024.09.17 |
| 【물리화학1】 5장 단순 혼합물 | 2024.09.15 |
| 【물리화학1】 4-2 상 전이의 열역학적 양상 | 2024.09.15 |