0. 이전 이야기
5-5장에서는 용매, 용질 그리고 정규 용액의 활동도에 대하여 학습하였음
활동도는 이상 용액에서 벗어난 실제 용액을 다루기 위해 도입된 것으로 이를 통해 더 정확한 계산이 가능함
https://nate0707.tistory.com/90
【물리화학1】 5-5 활동도
0. 이전 이야기 5-2장에서 배웠던 혼합 Gibbs에너지를 통해 5-3장에서는 액체와 기체가 공존할 때 상평형 그림에 대하여 학습하였는데, 이들은 모두 2성분 계였음5-4장에서는 3성분 계의 상평형 그
nate0707.tistory.com
이온이 아닌 경우 그들간의 상호작용이 약하기 때문에 묽은 용액이라면 몰랄농도를 이용해도 괜찮지만
이온의 경우 그들간의 상호작용이 매우 크기때문에 정말 대단히 묽은 용액을 제외하고는 활동도를 이용해야 함
양이온 $M^+$의 화학 퍼텐셜을 $\mu_+$로, 음이온 $M^-$의 화학 퍼텐셜을 $\mu_-$로 나타낼 때 이상 용액의 Gibbs 에너지는 다음과 같음
$G_m^{idea}=\mu_+^{ideal}+\mu_-^{ideal}$
여기서 $\mu_J^{ideal}=\mu_J^{\theta}+RTlnx_J$
그러나 실제 용액에 대해서 $\mu_J^{ideal}=\mu_J^{\theta}+RTlna_J=\mu_J^{ideal}+RTln\gamma_J$이므로
$G_m=\mu_+ +\mu_- =\mu_+^{ideal}+\mu_-^{ideal}+RTln\gamma_+ +RTln\gamma_-=G_m^{idea}+RTln \gamma_+ \gamma_-$
1. 평균 활동도 계수
- 평균 활동도 계수 정의
실제 용액의 Gibbs 에너지 변화에 대한 양이온의 기여와 음이온의 기여를 분리시킬 수는 없음
따라서 평균 활동도 계수를 이용해 비이상성에 대한 두 이온의 책임을 똑같이 분담시킴
$\gamma_±=(\gamma_+ \gamma_-)^{1/2}$
$\mu_+=\mu_+^{ideal}+RTln\gamma_±$
$\mu_-=\mu_-^{ideal}+RTln\gamma_±$
이를 일반화 시켜 p개의 양이온과 q개의 음이온을 내놓는 $M_pX_q$에 적용시키면
$G_m=p\mu_+ +q\mu_- =\mu_+^{ideal}+\mu_-^{ideal}+pRTln\gamma_+ +qRTln\gamma_-=G_m^{ideal}+pRTln\gamma_+ +qRTln\gamma_-$
이때 $\gamma_±=(\gamma_+^p \gamma_-^q)^{1/(p+q)}$
$\mu_i=\mu_i^{ideal}+RTln\gamma_±$
- Debye-Huckel 극한의 법칙
전체적으로 봤을 때 용액은 중성이지만, 특정 이온을 관찰했을 때 그 주위에는 반대 전하의 이온이 더 많이 존재함
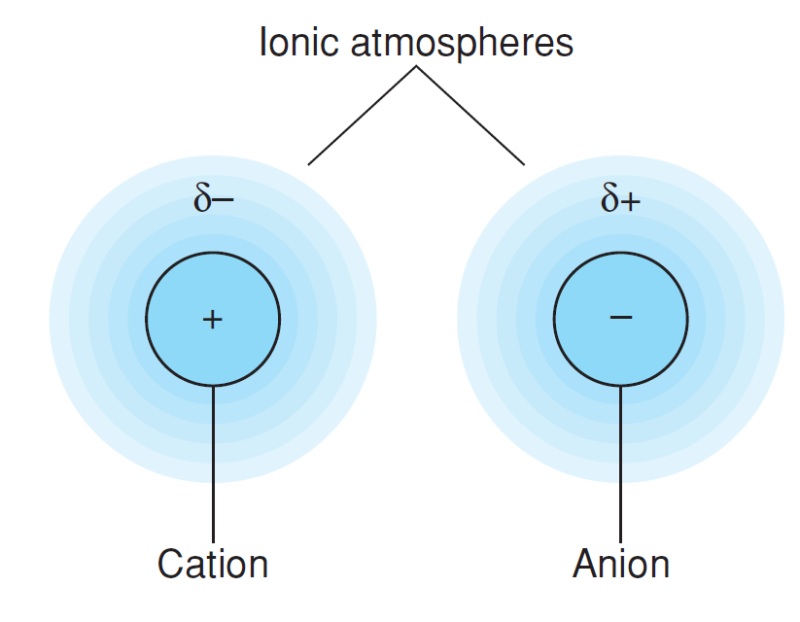
즉 한 이온 주위에는 같은 종류의 이온보다 반대 전하의 이온들이 수적으로 더 많기 때문에 한 이온 주위의 전하를 시간 평균하면 구형 안개 모양의 반대 전하가 생기는데, 이를 이온 분위기라고 함
중심 이온은 그 이온 분위기와 정전기적 상호작용을 통해 화학 퍼텐셜이 낮아짐
이때 낮아지는 에너지가 바로 $RTln\gamma_±$가 되는 것임
이때 활동도 계수는 다음과 같음
$log\gamma_±=-A|z_+z_-|I^{1/2}$ Debye-Huckel 극한 법칙
25℃에서 A=0.509이며 I는 용액의 이온세기임
$I=\frac{1}{2} \sum_i z_i^2(b_i/b^{\theta})$
여기서 $z_i$는 이온 i의 전하수이고 $b_i$는 몰랄 농도임
- 극한 법칙의 확장
용액의 이온 세기 I가 높아서 극한 법칙이 성립하지 않을때는 확장된 Debye-Huckel 법칙을 이용해 활동도 계수를 구함
$log\gamma_±=-\frac{A|z_+z_-|I^{1/2}}{1+BI^{1/2}}$ 확장된 Debye-Huckel
여기서 더 유연한 확장식은 Davies 식임
$log\gamma_±=-\frac{A|z_+z_-|I^{1/2}}{1+BI^{1/2}}+CI$ Davies 식
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 6-1 평형 상수 (0) | 2024.09.21 |
|---|---|
| 【물리화학1】 6장 화학 평형 (1) | 2024.09.20 |
| 【물리화학1】 5-5 활동도 (0) | 2024.09.19 |
| 【물리화학1】 5-4 3성분 계의 상평형 그림 (0) | 2024.09.18 |
| 【물리화학1】 5-3 2성분 계의 상평형 그림 (0) | 2024.09.18 |