0. 이전이야기
엔트로피를 이용하여 자발성을 따질 경우 계와 주위의 엔트로피를 모두 조사하여야 함
따라서 이를 간편화하기 위해 계만을 조사해서 자발성을 따질 수 있는 Helmholtz 에너지와 Gibbs 에너지에 대해 이야기함
이 두가지는 Clausius 부등식을 변형하여 생긴 식으로 특정 조건 하에서 과정이 자발성을 갖는 것을 보여줌
* $dS-\frac{dU}{T}≥0$ Clausius 부등식
$A=U−TS$ Helmholtz 에너지의 정의
$G=H−TS$ Gibbs 에너지의 정의
$dA_{T,V}≤0$ , $dG_{T,p}≤0$ 의 조건일 때 자발적임
이러한 Helmholtz 에너지와 Gibbs 에너지의 변화량을 통해 각각 최대일과 비-팽창일을 구할 수 있음
$w_{max}=\Delta A$ , $w_{add,max}=\Delta G$
또한 엔트로피와 엔탈피처럼 Gibbs에너지를 이용하여 표준 몰 Gibbs 에너지를 정의하고 표준 반응 Gibbs 에너지와 표준 생성 Gibbs 에너지를 통해 과정의 자발성을 확인할 수 있음
https://nate0707.tistory.com/80
【물리화학1】 3-3 계를 주목할 때
0. 이전이야기 이전 포스팅에서는 엔트로피의 측정에 대하여 다뤘음엔트로피를 측정할 때는 대기압에서의 측정을 가정하며 각 구간에서의 상전이 엔트로피를 고려해줘야함$S_m(T)=S_m(0)$ $+\int_0^{
nate0707.tistory.com
열역학 제 1법칙에 의하면 $dU=dq+dw$
닫힌계에서 가역적 변화가 일어나고 비-팽창일이 없다면 $dq_{rev}=-pdV$ , $dq_{rev}=TdS$
따라서 $dU=TdS-pdV$ 열역학 1법칙과 2법칙을 합쳐놓은 기본 식
* dU는 완전 미분이므로 그 값은 경로에 무관하고 따라서 가역적이건 비가역적이건 상관 없음
1. 내부 에너지의 성질
위의 기본식에 의하면 U=U(S,V)이므로 $dU=(\frac{\partial U}{\partial S})_V dS+(\frac{\partial U}{\partial V})_S dV$
이를 기본식과 비교하면 $(\frac{\partial U}{\partial S})_V=T$ $(\frac{\partial U}{\partial V})_S=-p$
- Maxwell 방정식
$f(x,y)$의 미소 변화는 $df=g(x,y)dx+h(x,y)dy$로 나타낼 수 있음
만약 완전 미분이 되려면, $g=(\partial f/ \partial x)_y$이고 $h=(\partial f / \partial y)_x$
이를 정리하면 $(\frac{\partial g}{\partial y})_x=(\frac{\partial h}{\partial x})_y$
이를 $dU=TdS-pdV$에 적용시키면
$(\frac{\partial T}{\partial V})_S=-(\frac{\partial p}{\partial S})_V$ Maxwell 관계식 중 하나
* $dU=TdS-pdV$의 식에서, S를 고정시키고 T를 V에대해 미분 = V를 고정시키고 -p를 S에 대해 미분
★중요★ 이러한 Maxwell 관계식을 엔탈피 H, 깁스 에너지 G, 헬름혼츠 에너지 A에 대해 적용하면 다음과 같음
| 상태함수 | 완전 미분 | Maxwell 관계식 |
| U | dU=TdS-pdV | $(\frac{\partial T}{\partial V})_S=-(\frac{\partial p}{\partial S})_V$ |
| H | dH=TdS-Vdp | $(\frac{\partial T}{\partial p})_S=(\frac{\partial V}{\partial S})_p$ |
| A | dA=-pdV-SdT | $(\frac{\partial p}{\partial T})_V=(\frac{\partial S}{\partial V})_T$ |
| G | dG=Vdp-SdT | $(\frac{\partial V}{\partial T})_p=(\frac{\partial S}{\partial p})_T$ |
Q) Maxwel 관계식을 이용하여 완전 기체의 엔트로피가 $lnV$에 비례함을 보이시오
A) 위의 도표에 따르면, $(\frac{\partial p}{\partial T})_V=(\frac{\partial S}{\partial V})_T$
$(\frac{\partial p}{\partial T})_V=(\frac{\partial (nRT/V)}{\partial T})_V=\frac{nR}{V}$
즉, $(\frac{\partial S}{\partial V})_T=\frac{nR}{V}$
$\int dS=nR \int \frac{dV}{V}=nRlnV+constant$
- 내부 에너지의 부피에 따른 변화
2-4장 상태함수에서 T와 V에 따른 U의 변화를 정의한 적 있음
$dU=(\frac{\partial U}{\partial V})_TdV+(\frac{\partial U}{\partial T})_VdT$
여기서 각각의 비례 상수들은 의미를 갖고 있었는데,
dT의 비례상수인 $(\frac{\partial U}{\partial T})_V$는 일정-부피 열용량 $C_V$이고
dV의 비례상수인 $(\frac{\partial U}{\partial V})_T$는 한 물질의 내부 에너지가 일정 온도에서 그 부피에 어떻게 의존하는지를 나타내는 $\pi_T$ 임
* $\pi_T$는 압력과 동일한 단위를 갖지만, 시료 안의 분자들 사이의 상호작용 때문에 생기는 것이며 이 때문에 내부적 압력이라고 부름
이러한 $\pi_T$는 Maxwell식을 이용하여 새로운 열역학적 상태식이 됨
우선 처음의 $dU=(\frac{\partial U}{\partial S})_V dS+(\frac{\partial U}{\partial V})_S dV$ 식에서 등온에서 dV를 양변에 나눠줌
$(\frac{\partial U}{\partial V})_T=(\frac{\partial U}{\partial S})_V (\frac{\partial S}{\partial V})_T+(\frac{\partial U}{\partial V})_S$
이 식을 정리하면 $\pi_T=T(\frac{\partial S}{\partial V})_T-p$
https://nate0707.tistory.com/75
【물리화학1】 2-4 상태 함수와 완전 미분
0. 이전 이야기 저번 포스팅에서는 표준 엔탈피에 대하여 포스팅함엔탈피란 일정 압력에서의 열의 변화를 설명하는 개념인데이때 1bar의 압력하의 표준 상태에서의 변화인 표준 엔탈피를 많이
nate0707.tistory.com
Q) 완전 기체에 대해서는 $\pi_T=0$임을 보이고 van der Waals 기체의 식에 대한 값도 구하시오
A) $\pi_T=T(\frac{\partial S}{\partial V})_T-p$ , 여기서 $(\frac{\partial S}{\partial V})_T$를 변형하여 계산하면 됨
$(\frac{\partial p}{\partial T})_V=(\frac{\partial S}{\partial V})_T$이므로
$(\frac{\partial p}{\partial T})_V=(\frac{\partial (nRT/V)}{\partial T})_V=\frac{nR}{V}$
따라서 $\pi_T=\frac{nRT}{V}-p=0$
van der Waals 기체의 상태식은 $p=\frac{nRT}{V-nb}-a\frac{n^2}{V^2}$
이를 이용해 계산하면 $(\frac{\partial p}{\partial T})_V=\frac{nR}{V-nb}$
따라서 $\pi_T=\frac{nRT}{V-nb}-p=\frac{nRT}{V-nb}-(\frac{nRT}{V-nb}-a\frac{n^2}{V^2})=a\frac{n^2}{V^2}$
2. Gibbs 에너지의 성질
내부 에너지의 기본식처럼 Gibbs 에너지 G=H-TS 에도 똑같은 논리가 적용됨
- 일반적 고찰
일반적 상태해서 H, T, S 모두가 변하므로
$dG=dH-d(TS)=dH-TdS-SdT$
$H=U+pV$이므로 $dH=dU+d(pV)=dU+pdV+Vdp$
따라서 $dG=dU+pdV+Vdp-TdS-SdT$
비-팽창 일을 하지 않는 닫힌 계에서는 $dU=TdS-pdV$이므로
$dG=Vdp-SdT$ 화학 열역학의 기본식
이를 통해 G=G(p,T)를 알 수 있고
$dG=(\frac{\partial G}{\partial p})_T dp+(\frac{\partial G}{\partial T})_p dT$
즉 $(\frac{\partial G}{\partial p})_T=V$ , $(\frac{\partial G}{\partial T})_p=-S$ G의 T와 p에 따른 변화
이를 통해 여러 물리학적 해석이 도출됨
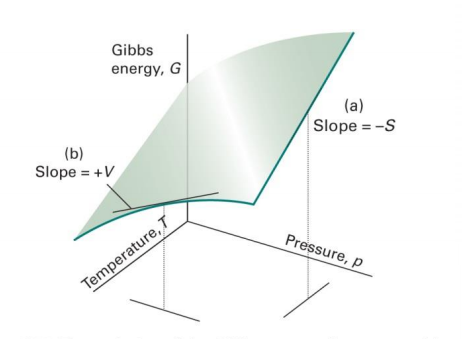
1. 어떤 물질에 대해서나 S>0이므로 온도가 올라가면(일정한 압력과 조성) G가 항상 감소함
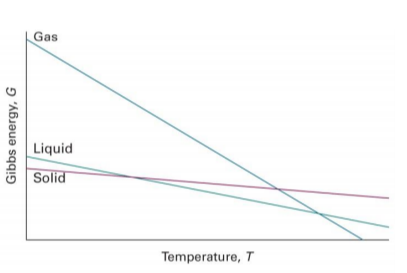
2. $(\frac{\partial G}{\partial T})_p$는 S가 증가할수록 더 크게 음이되며, 계의 엔트로피가 클 때는 G가 더 크게 감소해야함
* 따라서 높은 몰 엔트로피를 갖는 기체상 물질의 Gibbs 에너지는 온도에 더욱 예민함
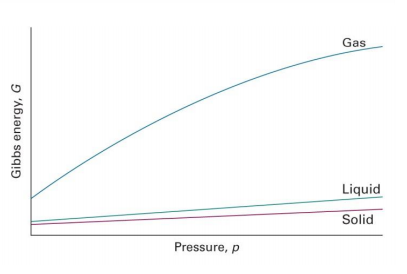
3. 어떤 물질에 대해서나 V>0이므로 계의 압력을 증가시키면(일정한 온도와 조성) 언제나 G가 증가함
4. $(\frac{\partial G}{\partial p})_T=V$이므로 계의 부피가 클 때(특히 기체일 경우) G가 압력 p에 더 예민함
- Gibbs 에너지의 온도에 따른 변화
계의 평형 조성은 그 계의 Gibbs 에너지에 의존함 그렇기에 온도에 따른 G의 변화를 살펴봐야함
* Gibbs 에너지 변화가 0일때 평형
$G=H-TS$이고 $-S=\frac{G-H}{T}$이므로
$(\frac{\partial G}{\partial T})_p=-S=\frac{G-H}{T}$
6장 화학평형 중 평형상수에 의하면 반응의 평형상수는 G보다 $\frac{G}{T}$와 관련됨
그렇기에 $\frac{G}{T}$의 온도 의존성, 즉 온도 T에대한 $\frac{G}{T}$의 변화량을 구해야함
$(\frac{\partial G/T}{T})_p=\frac{1}{T}(\frac{\partial G}{\partial T})_p+G\frac{d(1/T)}{dT}=\frac{1}{T}(\frac{\partial G}{\partial T})_p-\frac{G}{T^2}=\frac{1}{T} {(\frac{\partial G}{\ partial T})_p-\frac{G}{T}}$
즉 G/T의 온도 의존성을 구하기위해, G를 T에대해 미분하고 1/T도 T에대해 미분하여 꼴을 정리함
그리고 $(\frac{\partial G}{\partial T})_p=-S=\frac{G-H}{T}$의 꼴로 묶어서 다시 정리하면
$(\frac{\partial G/T}{T})_p=-\frac{H}{T^2}$ Gibbs-Helmholtz 식
이 식은 일정한 압력 하에서 일어나는 물리적 상태의 변화나 화학 반응과 같은 변화에 적용시키기 매우 적합함
위의 식을 다음처럼 변화량의 관점으로 다시 작성할 수 있음
$(\frac{\partial \Delta G/T}{T})_p=-\frac{\Delta H}{T^2}$
즉, 변화를 일으키고 있는 계의 엔탈피 변화를 통해 Gibbs 에너지가 온도에 따라 어떻게 변하는지 알 수 있음
- Gibbs 에너지의 압력에 따른 변화
온도가 일정할 경우 $dG=Vdp-SdT$에서 dT=0이므로 $dG=Vdp$
$G(p_f)=G(p_i)+\int_{p_i}^{p_f} Vdp$
이를 몰 양으로도 나타낼 수 있음
$G_m(p_f)=G_m(p_i)+\int_{p_i}^{p_f} V_mdp$
이 식은 물질이 어떤 상으로 있든 관계없이 적용되지만, 몰 부피 $V_m$이 압력에 어떻게 의존하는지 알아야 함
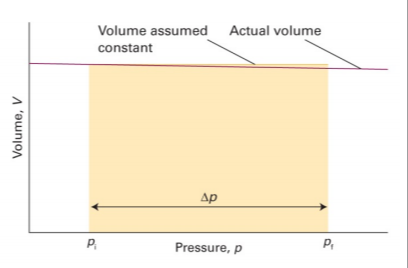
응축상의 물 보피는 압력이 변해도 거의 변하지 않으므로 $V_m$을 상수취급할 수 있음
$G_m(p_f)=G_m(p_i)+V_m \int_{p_i}^{p_f} dp=G_m(p_i)+(p_f-p_i)V_m$
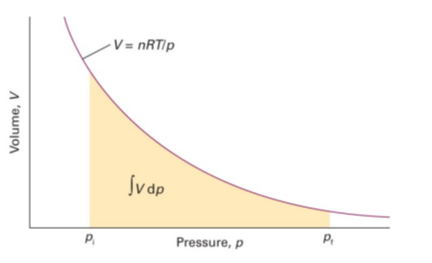
기체의 경우 몰 부피가 크며 몰부피는 압력에 의존함
따라서 완전기체의 경우 $V_m=RT/p$를 이용해 적분함
$G_m(p_f)=G_m(p_i)+RT \int_{p_i}^{p_f} \frac{1}{p} dp=G_m(p_i)+RTln\frac{p_f}{p_i}$
초기 압력 $p_i=p^{\theta}$ , 1bar의 표준압력으로 설정하면 아래의 식이 성립함
$G_m(p)=G_m^{\theta}+RTln\frac{p}{p^{\theta}}$ 완전 기체의 몰 Gibbs 에너지
- 퓨가시티
퓨가시티는 이상적인 기체로 만들어진 $G_m(p)=G_m^{\theta}+RTln\frac{p}{p^{\theta}}$ 식에 실제 계에 적용한 것으로
진짜 압력 p 대신 유효압력 f을 이용해 이상적 행동으로부터의 이탈을 매우 간단히 처리함
$G_m(p)=G_m^{\theta}+RTln\frac{f}{p^{\theta}}$
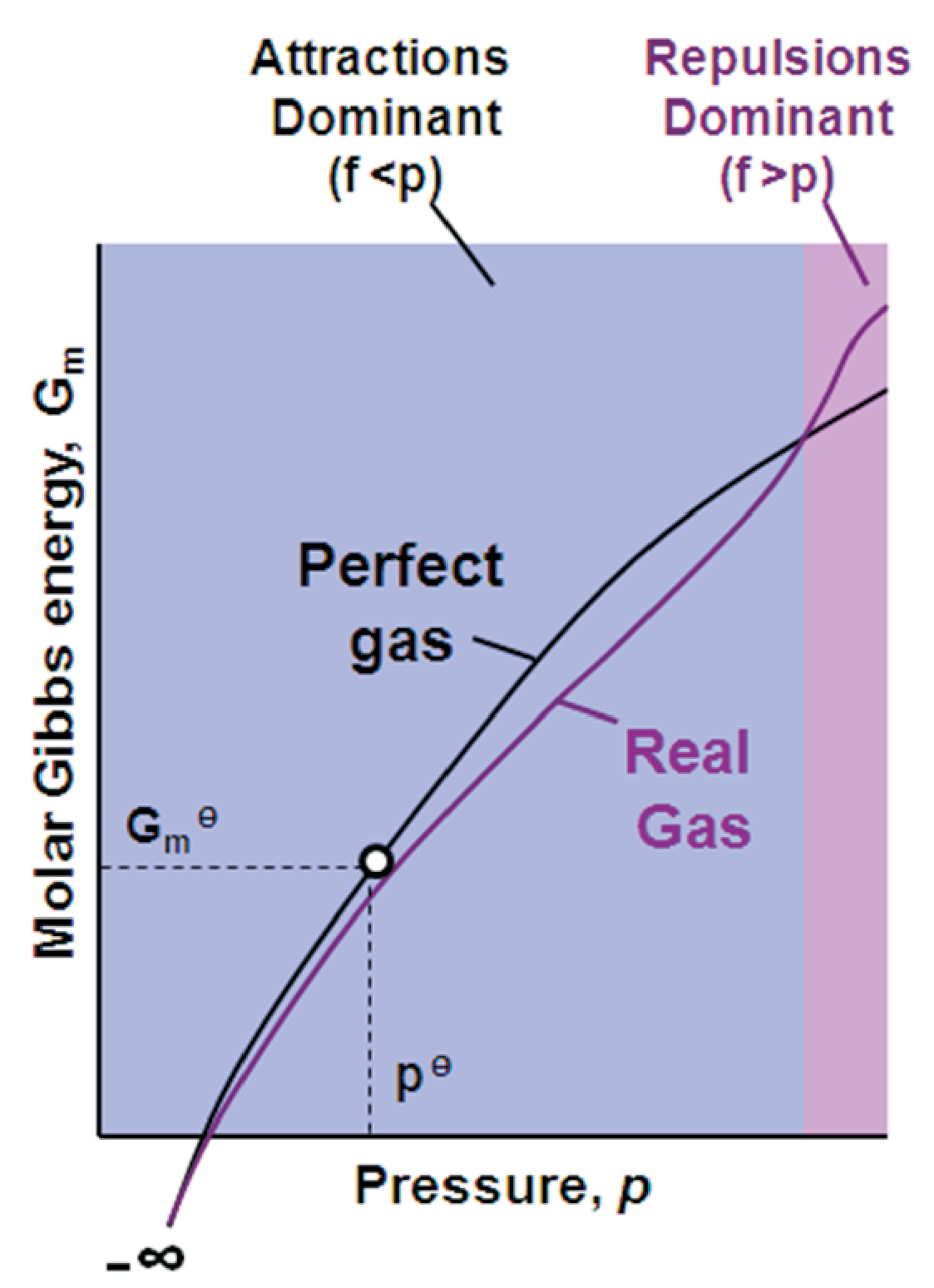
인력이 지배적일 경우 압력은 이상기체에 비해 감소할 것이므로 f<p
반발력이 지배적일 경우 압력은 이상기체에 비해 증가할 것이므로 f>p
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 4-1 순수한 물질의 상평형 그림 (0) | 2024.09.15 |
|---|---|
| 【물리화학1】 4장 순수한 물질의 물리적 변환 (0) | 2024.09.15 |
| 【물리화학1】 3-3 계를 주목할 때 (0) | 2024.09.12 |
| 【물리화학1】 3-2 엔트로피의 측정 (1) | 2024.09.09 |
| 【물리화학1】 3-1 엔트로피 (1) | 2024.09.08 |