0. 이전 이야기
이전 포스팅에서는 엔트로피에 대해 다뤘음
고립계의 전체에너지는 변화하지 않지만, 이는 언제나 에너지의 무작정한 꼴로의 분산이 수반됨
고립계가 자발적 변화를 일으키면 그 과정에서의 엔트로피는 증가해야 함 $\Delta S_{tot}>0$
엔트로피는 열역학적으로 정의되기도 하며 $dS=\frac{dq_{rev}}{T}$
통계 역학적으로 정의되기도 함 $S=klnW$
엔트로피의 주요 특징 중 하나는 이것이 상태함수라는 것임, 상태함수이기 위해서는 순환에 걸쳐 적분한 값이 0이어야함
이를 증명하기위해 Carnot 순환을 이용함
Clausius 부등식을 통해 엔트로피를 정의할 수 도 있음 $dq_{rev}/T=dS이므로 dS≥dq/T$
엔트로피 변화는 팽창, 상 전이, 가열, 복합과정 등에서 발생하며 각각 적합한 식을 통해 엔트로피의 변화를 구하고 과정의 자발성을 판단할 수 있음
https://nate0707.tistory.com/78
【물리화학1】 3-1 엔트로피
열역학 제 1법칙에 따르면 고립계의 전체 에너지는 변하지 않음하지만 이것은 다른 방식으로 분배되는데 자발적 변화는 언제나 에너지의 무작정한 꼴로의 분산을 수반함 1. 2법칙 열역학 제 2
nate0707.tistory.com
엔트로피를 측정하는 방법에는 시료의 온도를 T=0으로부터 관심 대상 온도까지 올려주는데 필요한 열-계량법과
계산된 파라미터나 분광학적 데이터를 이용하고 Boltzmann의 통계 역학적 정의를 이용하는 방법이 있음
이번 포스팅에서는 첫번째 방법을 통해 엔트로피를 측정하는 법을 알아볼 것임
1. 엔트로피의 열-계량 측정법
엔트로피를 측정할 때는 대기압에서의 측정을 가정하며 각 구간에서의 상전이 엔트로피를 고려해야만 함
$S_m(T)=S_m(0)$ $+\int_0^{T_f} {\frac{C_{p,m}(s,T}{T}dT}$ $+\frac{\Delta_{fus}H}{T_f}$ $+\int_{T_f}^{T_b} {\frac{C_{p,m}(l,T}{T}dT}$ $+\frac{\Delta_{vap}H}{T_b}$ $+\int_{T_b}^{T} {\frac{C_{p,m}(g,T}{T}dT}$
이때 $S_m(0)$을 제외한 모든 양들은 열-계량법으로 측정 가능함
또 이러한 적분들은 그래프 방식으로 구할 수 있음
이때 그때까지 일어난 상전이 엔트로피들을 더해야함
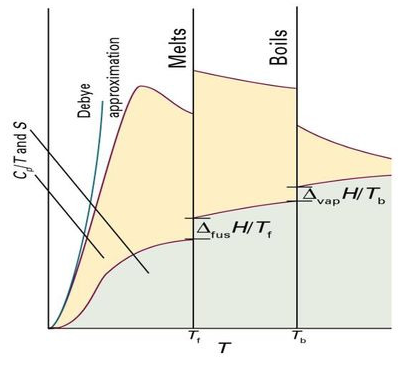
엔트로피 측정과 관련된 한 가지 문제는 T=0 절대온도 근처에서 열용량을 측정하기가 어렵다는 것임
하지만 T가 낮을 때는 열용량이 $T^3$에 비례하기에 Debye 외삽법을 이용함
2. 3법칙
- Nernst의 열 정리
Nernst의 열 정리
물리적이나 화학적 변환에 수반되는 엔트로피 변화는 절대 영도로 접근함에 따라 0으로 접근함
즉 관련된 물질들이 모두 완전한 질서적 배열을 이룬다면 $T→0$일 때 $\Delta S→0$임
* 여기서 Boltzmann equation을 생각해볼 수 있음, S=klnW에서 완전한 질서적 배열은 W=1을 의미하므로 S=0임
이 Nernst의 열 정리에 의하면, T=0에서 완전한 결정 상태로 있는 원소의 엔트로피 값을 임의로 0으로 놓으면, 이러한 상태의 화합물의 엔트로피도 0이됨
* 화합물 생성에 수반되는 엔트로피 변화는(상전이 엔트로피처럼) 0이되므로
즉, 이를 정리하여 열역학 제 3법칙을 얻을 수 있음
모든 완전한 결정 물질의 엔트로피는 T=0에서 0임
하지만 어떤 경우에는 T=0에서 W>1이 되어 S(0)>0인 경우가 존재함 하지만 이때도 에너지 차가 거의 없음
예를 들어 2원자 분자 AB의 경우 AB,AB,AB의 배치와 BA,AB,BA의 배치를 갖음
얼음또한 비슷한 경우인데, 이는 2개의 짧은 결합과 2개의 긴 결합의 경우의수 때문임
이러한 물질들은 잔류 엔트로피를 갖는다고 말함
이러한 잔류 엔트로피는 $S=klnW$를 이용하여 추산할 수 있음
- 3법칙
S(0)=0으로 맞춘 엔트로피를 3법칙 엔트로피라고 부름
온도 T에서 표준 상태에 있는 물질의 3법칙 엔트로피는 표준(3법칙) 엔트로피라고 하며 $S^{\Theta}(T)$로 표시함
명시된 온도에서 순수하게 분리된 상태로 있는 생성물들과 반응물들 사이의 엔트로피 차를 표준 반응 엔트로피라고 정의
$\Delta_r S^{\Theta}=\sum_{products}{vS_m^{\Theta}}-\sum_{reactants}{vS_m^{\Theta}}$
이를 정리하면
$\Delta_r S^{\Theta}=\sum_{J}{v_JS_m^{\Theta}(J)}$
여기서 $v_J$는 화학량적 수로 생성물에 대해서는 +, 반응물에 대해서는 -를 갖음
반응에서 기체가 실질적으로 생성될 때는 엔트로피가 양이 되고, 기체가 소모될 때는 음이되기 쉬움
*기체가 생성된다는 것은 부피가 증가하고 자발성이 커진다는 뜻이므로
# 이온의 엔트로피
2-3 열화학에서 엔탈피에서 설명했듯이 음이온이 없는 양이온만의 용액을 만들 수 없음
이때 이온의 표준 생성 엔탈피를 임의로 정의했던 것 처럼, 이온의 표준 몰 엔트로피 또한 물속의 $H^+$ 이온의 표준 엔트로피를 모든 온도에서 0으로 정의함
$S^{\Theta}(H^+,aq)=0$
https://nate0707.tistory.com/73?category=1449137
【물리화학1】 2-3 열화학
0. 이전 이야기 저번 포스팅에서는 엔탈피에 대해서 학습함엔탈피란 일정한 압력하에서 열의 변화를 설명하기 위핸 개념등압과정에서 열의 변화 ≠ 내부에너지 변화 이므로 새로운 정의를 한
nate0707.tistory.com
물속에 있는 이온의 엔트로피는 물속에 있는 수소 이온을 기준으로한 상대값이므로 이 값은 양과 음 모두가 될 수 있음
이때 이온의 전하밀도(Charge density)가 크면 주변 물분자가 질서정연하며 엔트로피가 작음 $Cl^-=57Jk^{-1}mol ^{-1}$
이온의 전하밀도가 작으면 주변 물분자가 느슨해서 엔트로피가 큼 $mg^{2+}=-128Jk^{-1}mol ^{-1}$
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 3-4 1법칙과 2법칙의 결합 (4) | 2024.09.13 |
|---|---|
| 【물리화학1】 3-3 계를 주목할 때 (0) | 2024.09.12 |
| 【물리화학1】 3-1 엔트로피 (1) | 2024.09.08 |
| 【물리화학1】 3장 2법칙과 3법칙 (2) | 2024.09.07 |
| 【물리화학1】 2-5 단열 변화 (4) | 2024.09.07 |
0. 이전 이야기
이전 포스팅에서는 엔트로피에 대해 다뤘음
고립계의 전체에너지는 변화하지 않지만, 이는 언제나 에너지의 무작정한 꼴로의 분산이 수반됨
고립계가 자발적 변화를 일으키면 그 과정에서의 엔트로피는 증가해야 함 $\Delta S_{tot}>0$
엔트로피는 열역학적으로 정의되기도 하며 $dS=\frac{dq_{rev}}{T}$
통계 역학적으로 정의되기도 함 $S=klnW$
엔트로피의 주요 특징 중 하나는 이것이 상태함수라는 것임, 상태함수이기 위해서는 순환에 걸쳐 적분한 값이 0이어야함
이를 증명하기위해 Carnot 순환을 이용함
Clausius 부등식을 통해 엔트로피를 정의할 수 도 있음 $dq_{rev}/T=dS이므로 dS≥dq/T$
엔트로피 변화는 팽창, 상 전이, 가열, 복합과정 등에서 발생하며 각각 적합한 식을 통해 엔트로피의 변화를 구하고 과정의 자발성을 판단할 수 있음
https://nate0707.tistory.com/78
【물리화학1】 3-1 엔트로피
열역학 제 1법칙에 따르면 고립계의 전체 에너지는 변하지 않음하지만 이것은 다른 방식으로 분배되는데 자발적 변화는 언제나 에너지의 무작정한 꼴로의 분산을 수반함 1. 2법칙 열역학 제 2
nate0707.tistory.com
엔트로피를 측정하는 방법에는 시료의 온도를 T=0으로부터 관심 대상 온도까지 올려주는데 필요한 열-계량법과
계산된 파라미터나 분광학적 데이터를 이용하고 Boltzmann의 통계 역학적 정의를 이용하는 방법이 있음
이번 포스팅에서는 첫번째 방법을 통해 엔트로피를 측정하는 법을 알아볼 것임
1. 엔트로피의 열-계량 측정법
엔트로피를 측정할 때는 대기압에서의 측정을 가정하며 각 구간에서의 상전이 엔트로피를 고려해야만 함
$S_m(T)=S_m(0)$ $+\int_0^{T_f} {\frac{C_{p,m}(s,T}{T}dT}$ $+\frac{\Delta_{fus}H}{T_f}$ $+\int_{T_f}^{T_b} {\frac{C_{p,m}(l,T}{T}dT}$ $+\frac{\Delta_{vap}H}{T_b}$ $+\int_{T_b}^{T} {\frac{C_{p,m}(g,T}{T}dT}$
이때 $S_m(0)$을 제외한 모든 양들은 열-계량법으로 측정 가능함
또 이러한 적분들은 그래프 방식으로 구할 수 있음
이때 그때까지 일어난 상전이 엔트로피들을 더해야함

엔트로피 측정과 관련된 한 가지 문제는 T=0 절대온도 근처에서 열용량을 측정하기가 어렵다는 것임
하지만 T가 낮을 때는 열용량이 $T^3$에 비례하기에 Debye 외삽법을 이용함
2. 3법칙
- Nernst의 열 정리
Nernst의 열 정리
물리적이나 화학적 변환에 수반되는 엔트로피 변화는 절대 영도로 접근함에 따라 0으로 접근함
즉 관련된 물질들이 모두 완전한 질서적 배열을 이룬다면 $T→0$일 때 $\Delta S→0$임
* 여기서 Boltzmann equation을 생각해볼 수 있음, S=klnW에서 완전한 질서적 배열은 W=1을 의미하므로 S=0임
이 Nernst의 열 정리에 의하면, T=0에서 완전한 결정 상태로 있는 원소의 엔트로피 값을 임의로 0으로 놓으면, 이러한 상태의 화합물의 엔트로피도 0이됨
* 화합물 생성에 수반되는 엔트로피 변화는(상전이 엔트로피처럼) 0이되므로
즉, 이를 정리하여 열역학 제 3법칙을 얻을 수 있음
모든 완전한 결정 물질의 엔트로피는 T=0에서 0임
하지만 어떤 경우에는 T=0에서 W>1이 되어 S(0)>0인 경우가 존재함 하지만 이때도 에너지 차가 거의 없음
예를 들어 2원자 분자 AB의 경우 AB,AB,AB의 배치와 BA,AB,BA의 배치를 갖음
얼음또한 비슷한 경우인데, 이는 2개의 짧은 결합과 2개의 긴 결합의 경우의수 때문임
이러한 물질들은 잔류 엔트로피를 갖는다고 말함
이러한 잔류 엔트로피는 $S=klnW$를 이용하여 추산할 수 있음
- 3법칙
S(0)=0으로 맞춘 엔트로피를 3법칙 엔트로피라고 부름
온도 T에서 표준 상태에 있는 물질의 3법칙 엔트로피는 표준(3법칙) 엔트로피라고 하며 $S^{\Theta}(T)$로 표시함
명시된 온도에서 순수하게 분리된 상태로 있는 생성물들과 반응물들 사이의 엔트로피 차를 표준 반응 엔트로피라고 정의
$\Delta_r S^{\Theta}=\sum_{products}{vS_m^{\Theta}}-\sum_{reactants}{vS_m^{\Theta}}$
이를 정리하면
$\Delta_r S^{\Theta}=\sum_{J}{v_JS_m^{\Theta}(J)}$
여기서 $v_J$는 화학량적 수로 생성물에 대해서는 +, 반응물에 대해서는 -를 갖음
반응에서 기체가 실질적으로 생성될 때는 엔트로피가 양이 되고, 기체가 소모될 때는 음이되기 쉬움
*기체가 생성된다는 것은 부피가 증가하고 자발성이 커진다는 뜻이므로
# 이온의 엔트로피
2-3 열화학에서 엔탈피에서 설명했듯이 음이온이 없는 양이온만의 용액을 만들 수 없음
이때 이온의 표준 생성 엔탈피를 임의로 정의했던 것 처럼, 이온의 표준 몰 엔트로피 또한 물속의 $H^+$ 이온의 표준 엔트로피를 모든 온도에서 0으로 정의함
$S^{\Theta}(H^+,aq)=0$
https://nate0707.tistory.com/73?category=1449137
【물리화학1】 2-3 열화학
0. 이전 이야기 저번 포스팅에서는 엔탈피에 대해서 학습함엔탈피란 일정한 압력하에서 열의 변화를 설명하기 위핸 개념등압과정에서 열의 변화 ≠ 내부에너지 변화 이므로 새로운 정의를 한
nate0707.tistory.com
물속에 있는 이온의 엔트로피는 물속에 있는 수소 이온을 기준으로한 상대값이므로 이 값은 양과 음 모두가 될 수 있음
이때 이온의 전하밀도(Charge density)가 크면 주변 물분자가 질서정연하며 엔트로피가 작음 $Cl^-=57Jk^{-1}mol ^{-1}$
이온의 전하밀도가 작으면 주변 물분자가 느슨해서 엔트로피가 큼 $mg^{2+}=-128Jk^{-1}mol ^{-1}$
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 3-4 1법칙과 2법칙의 결합 (4) | 2024.09.13 |
|---|---|
| 【물리화학1】 3-3 계를 주목할 때 (0) | 2024.09.12 |
| 【물리화학1】 3-1 엔트로피 (1) | 2024.09.08 |
| 【물리화학1】 3장 2법칙과 3법칙 (2) | 2024.09.07 |
| 【물리화학1】 2-5 단열 변화 (4) | 2024.09.07 |