열역학 제 1법칙에 따르면 고립계의 전체 에너지는 변하지 않음
하지만 이것은 다른 방식으로 분배되는데 자발적 변화는 언제나 에너지의 무작정한 꼴로의 분산을 수반함
1. 2법칙
열역학 제 2법칙은 어떤 과정이 자발적이고 어떤 것이 비-자발적인지 발혀줌
Kelvin은 열역학 제 2법칙을 다음과 같이 표현함
$열원으로부터 열을 흡수하고 이 열을 전부 오로지 일로만 변화시키는 과정은 불가능하다$
즉 열기관에서 열을 일로 변환할때, 일부 에너지가 일로 변환되지 않고 그대로 열로서 수채로 빠져나간다는 것임
* 전체 에너지가 분산되는 변화 방향으로 간다는 뜻
Rudolf Clausius는 열역학 제 2법칙을 다음과 같이 표현함
$열은 찬 물체로부터 뜨거운 물체로 자발적으로 흐르지 않는다$
엔트로피를 이용하면 어떤 변화가 자발적인지 여부를 판단할 수 있음
$고립계가 자발적 변화를 일으키면 그 과정에서 계의 엔트로피가 증가해야 한다 \Delta S_{tot}>0$
여기서 $\Delta S_{tot}$은 계와 주위와의 전체 엔트로피
열역학적 비가역 과정은 자발적 과정이며 엔트로피 증가가 수반되어야함
2. 엔트로피의 정의
- 엔트로피의 열역학적 정의
내부에너지는 열과 일로 구성됨
이 중 일은 주위에 있는 원자들의 균일한 운동을 자극시키므로 엔트로피를 변화시키지 않음
즉, 엔트로피 변화 dS = 에너지가 분산되는 정도의 변화 = 얼마나 많은 에너지가 열로 이전되는가
$dS=\frac{dq_{rev}}{T}$ 엔트로피 변화의 정의
$\Delta S=\int_i^f{\frac{q_{rev}}{T}}$
즉 계의 임의 두 상태 사이의 엔트로피 차는 두 상태의 가역적 경로에서 열로서 공급되는 에너지를 온도로 나누어 적분해야함
- 완전기체 등온 팽창의 엔트로피 변화
Q) 완전 기체가 $V_i$로부터 $V_f$로 등온 팽창할 때의 엔트로피 변화는?
A) 처음과 최종상태 사이의 가역적 경로에서 흡수되는 열을 알아야 함
등온 팽창이므로 $\Delta U=q+w$에서 $\Delta U=0$이고 $q=-w$이며 $q_{rev}=-w_{rev}=nRTln\frac{V_f}{V_i}$
$\Delta S=\frac{1}{T} \int_i^f{dq_{rev}}=\frac{q_{rev}}{T}=nRln\frac{V_f}{V_i}$ $\Delta S_m=Rln\frac{V_f}{V_i}$
- 주위의 엔트로피 변화
$dS=\frac{dq_{rev}}{T}$ 를 이용하면 주위의 엔트로피 변화 $\Delta S_{sur}$ 도 구할 수 있음
주위는 일정한 부피의 열원으로 w=0임 이때 가열로써 공급된 에너지 = $dU_{sur}$
이때 $dU_{sur}$은 상태함수 이므로 이 변화가 가역적이건 비가역적이건 관계 없음
$dS=\frac{dq_{rev,sur}}{T_{sur}}=\frac{dq_{sur}}{T_{sur}}$
또한 어떤 변화에도 주위의 온도는 일정하므로 $\Delta S_{sur}=\frac{q_{sur}}{T_{sur}}$
- 엔트로피의 통계 역학적 정의
볼츠만은 계의 엔트로피를 에너지 준위 상의 분자 분포와 연관시킴
$S=klnW$ 엔트로피에 대한 Boltzmann식
이때 $k=1.381\times10^{-23}JK^{-1}$이고 W는 미시적 상태의 수 즉 가능한 분자 배치의 수임
물질과 에너지가 더 무질서하게 분포될수록 그 총 에너지에 대응하는 미시적 상태 W가 커짐
# 에너지 준위 수와 미시적 상태 W
분자들이 접근할 수 있는 에너지 준위의 수가 많아지면 주어진 전체 에너지를 이루는 방법이 많아져 미시적 상태 W가 커짐
온도가 높은 계의 분자들은 이미 많은 수의 가용 에너지 준위를 점유하여 열로서 에너지를 가해주어도 점유되는 에너지 준위의 수가 조금 밖에 증가하지 않음 따라서 미시적 상태의 수 W가 크게 늘지 않아 엔트로피도 크게 변화하지 않음
하지만 온도가 낮은 분자들은 훨씬 적은 수의 에너지 준위를 갖고 있어 같은 양의 에너지를 가해도 허용되는 에너지 준위의 수가 크게 늘어나 미시적 상태의 수 W가 크게 늘어 엔트로피가 크게 변화함
3. 상태함수로서의 엔트로피
엔트로피는 상태함수인데 이를 증명하기 위해서는 dS의 적분이 경로에 무관하다는 것을 보여야함
첫번째로 이상기체의 특정 순환)Carnot)에 대해서 dS의 적분이 경로에 무관하다는 것을 보이며
두번째로는 이상기체 뿐 아니라 다른 어떠한 물질에서도 dS의 적분이 경로에 무관하다는 것을 보이고
마지막으로 특정순환(Carnot)이 아닌 모든 순환에 대해 dS의 적분이 경로에 무관하다는 것을 보일 것임
- Carnot 순환
엔트로피가 상태함수임을 증명하기 위해 순환에 걸쳐 적분한 결과값이 0임을 보여야함
A→B→C→D→A의 엔트로피 변화의 합이 0이어야함
카르노 순환은 네가지 가역 단계로 이뤄짐

1. 등온 가역 팽창

2. 단열 가역 팽창

3. 등온 가역 압축

4. 단열 가역 압축
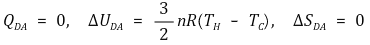
이때 이 네과정의 엔트로피 합을 구하면 다음과 같음
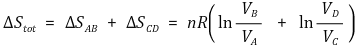
단열과정에서 완전 기체의 가역 팽창은 다음과 같은 식을 만족함

https://nate0707.tistory.com/76
【물리화학1】 2-5 단열 변화
0. 이전 이야기 저번 포스팅에서는 상태함수와 완전미분이라는 주제를 다뤘음내부 에너지와 엔탈피 모두 상태함수이기에 이들을 조작하여 열용량들 사이의 관계와 기체를 냉각시키는데 이용
nate0707.tistory.com
따라서 이를 정리하면

# 카르노기관의 열 효율
$\varepsilon=$ 행해진 일 / 뜨거운 열원으로부터 흡수된 열 $=\frac{|w|}{|q_h|}$
이 기관이 일로서 공급하는 에너지는 뜨거운 열원으로부터 받은 열과 저-열원으로 돌려준 열과의 차이임으로
$\varepsilon=\frac{|q_h|-|q_c|}{|q_h|}=1-\frac{|q_c|}{|q_h|}$
그런데 열역학 제 2법칙에 의하면 가역 기관은 어떤 것이나 그 구조에 관계없이 동일한 효율을 가져야 하므로 이상기체가 아니더라도 dS의 적분이 경로에 무관함
# 가역 기관은 어떤 것이나 동일한 효율을 가져야함 증명
만일 2개의 카르노사이클의 효율이 동일하지 않다고 하면, 한쪽을 순방향으로, 다른 쪽을 역방향으로 작동하도록 하여 연결시켜서 얻는 일이 공급하는 일과 같아지도록 소거시키면, 외부에 아무 변화도 남기지 않고 고온의 물체로 열을 공급하는 것이 가능함
하지만 이것은 영구기관으로 이는 불가능하므로, 이것은 존재할 수 없다. 따라서 2개의 카르노사이클의 효율은 동일해야함
이는 열역학 제 2법칙을 의미 : 저온의 물체로부터 고온의 물체로 열을 이동시키는 것 외에, 아무 변화도 남기지 않는 과정은 있을 수 없음
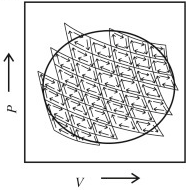
# 특정순환(Carnot)이 아닌 모든 순환에 대해 dS의 적분이 경로에 무관함을 증명
한 일반적 순환은 작은 Carnot 순환으로 나눌 수 있음(구분구적과 비슷함)
작은 Carnot 순환들의 집단 내부에서는 경로들이 상쇄되며 결국 주변들만 살아남고 이는 진짜 순환과 일치함
각각의 Carnot 순환에서 엔트로피의 변화는 0이므로 일반적 순환의 엔트로피 변화도 0이됨
$\sum_{all} {\frac{q_{rev}}{T}} = \sum_{perimeter} {\frac{q_{rev}}{T}}$
- 열역학적 온도
온도가 $T_h$인 열원과 온도가 T인 찬 열-수채 사이에서 작동하는 기관은 다음 식을 만족함
$T=(1-\varepsilon)T_h$
Kelvin은 이 식을 이용해 삼중점 하에 있는 물(273.16K)을 뜨거운 열원으로 사용하는 척도를 정함
이때 열기관의 효율 $\varepsilon$만 구하면 찬 열-수채의 온도 T를 구할 수 있음
- Clausius 부등식
엔트로피의 정의가 2법칙을 부합함을 Clausius 부등식을 통해 보일 수 있음
우선 팽창을 할때 비-가역적 조건보다 가역적 조건에서 더 많은 일이 행해짐
* 팽창 시 각 단계에서 외부 압력을 내부 압력에 맞춰줌으로써 계는 미는 힘을 조금도 낭비시키지 않았기에 가역 과정이 비가역 과정보다 많은 일을 얻을 수 있음
https://nate0707.tistory.com/71
【물리화학1】 2-1 내부 에너지
열역학 제 1법칙 : 고립계의 총 에너지는 일정하다 1. 일, 열, 및 에너지 - 기초 정의 # 계와 주위 계 (system) : 우리가 관심을 갖는 부분주위 (surrounding) : 계 밖의 나머지 부분 # 여러가지 계 열린
nate0707.tistory.com
즉 $|dw_{rev}| ≥ |dw|$이고 엔어지가 계를 빠져나가면서 일을 할 때 이들은 모두 음수이므로 $-dw_{rev} ≥-dw$이고
정리하면 $dw-dw_{rev} ≥0$
한편 내부에너지는 상태함수이므로 동일한 두 상태 사이에서는 경로가 가역적이건 비가역적이건 상관이 없음
$dU=dq+dw=dq_{rev}+dw_{rev}$
$dq_{rev}-dq=dw-dw_{rev}≥0$ 즉 $dq_{rev}≥dq$가되어 양 변에 T로 나누면 $dq_{rev}/T≥dq/T$가 됨
$dq_{rev}/T=dS$이므로 $dS≥\frac{dq}{T}$ Clausius 부등식
가역과정일때 엔트로피변화 = 0
비가역과정일때 엔트로피 변화 ≥0
만약 계가 주위로부터 고립되어있어 dq=0일 경우 Clausius 부등식에 의해 dS≥0임
즉 고립계 안에서 자발적 변화가 일어날 때는 엔트로피가 감소할 수 없음
4. 특정 과정들에 수반되는 엔트로피 변화
- 팽창
부피가 $V_i$로부터 $V_f$로 등온 팽창하는 완전 기체의 엔트로피 변화는 다음과 같음
$\Delta S=nRln\frac{V_f}{V_i}$
이때 S는 상태함수이므로 이 계의 $\Delta S$값은 처음과 최종 상태들 사이의 경로에 무관하며 가역적이건 비가역적이건 상관 없음
하지만 가역변화에 대해서는 다음이 성립함
$\Delta S = \frac{q_{rev}}{T}=-nRln\frac{V_f}{V_i}$
즉 $\Delta S_{tot}=0$임을 알 수 있음
비가역변화일 경우 등온 팽창이 자유롭게
등온 팽창이 자유롭게 일어날 경우 $w=0$이고 등온이므로 $\Delta U=0$이므로 $q=0$임
* 주위는 계에 비해 크기가 매우 거대해 부피변화가 없어 w=0
즉 $\Delta S_{sur}=0$이므로 $\Delta S_{tot}=nRln\frac{V_f}{V_i}$
- 상 전이
전이 온도에서는 계의 두 상이 평형을 이루고 있으므로 계와 그 주위 사이에서 열로서 에너지 이전이 일어난다면 이것은 가역적임
이때 일정한 압력 하에서 $q=\Delta_{trs}H$이므로 이 계의 몰 엔트로피 변화는 다음과 같음
$\Delta_{trs}S=\frac{\Delta_{trs}H}{T_{trs}}$ 전이 온도에서의 상 전이 엔트로피
전이온도에서 전체 엔트로피 변화는 0
발열과정(얼 때 혹은 응축될 때)에선 계의 dq가 음수이고 계의 엔트로피 변화도 음수지만 주위로 에너지가 열로서 이전되어 들어가기 때문에 총합은 0이됨
흡열과정(용융 혹은 증발)에선 계의 dq가 양수이고 계의 엔트로피 변화도 양수지만 주위의 엔트로피가 감소하므로 총합은 0이됨
# Trouton 규칙
이는 많은 종류의 액체들의 표준 증발 엔트로피가 대체로 비슷하다는 것임
이들은 약 $85JK^{-1}mol^{-1}$임
그러한 이유는 어떤 액체든 증발하여 기체가 될 때 대체로 비슷한 정도의 부피 변화가 나타나기 때문임
하지만 물의 표준 증발 엔트로피는$109.1JK^{-1}mol^{-1}$로 Trouton 규칙을 만족하지 않음
이는 물이 분자들 사이의 수소 결합으로 액체가 상당한 구조를 가지고 있기 때문에 기체가 되었을때 무질서도가 크게 증가하는 것임
- 가열
온도가 $T_i$에서 $T_f$로 변할 때 우리는 계의 엔트로피를 구할 수 있음
이때 주의할 점은 상전이가 없음을 가정함
$S(T_f)=S(T_i)+\int_{T_i}^{T_f} {\frac{dq_{rev}}{T}}$
특히 중요한 것은 계가 일정한 압력 하에서(대기압과 같이) 가열될 때의 엔트로피 변화임
이때 $C_p=(\partial H/\partial T)_p$를 $dq_{rev}=C_pdT$로 고쳐 사용할 수 있음
* $\partial H=dq_{rev}$이므로
$S(T_f)=S(T_i)+\int_{T_i}^{T_f} {\frac{C_pdT}{T}}$
$C_p$가 적분 영역에서 온도에 무관할 때를 가정하면
$S(T_f)=S(T_i)+C_p \int_{T_i}^{T_f} {\frac{dT}{T}}=S(T_i)+C_pln\frac{T_f}{T_i}$
즉 $\Delta S$는 $C_p$와 비례함
*즉 엔트로피 변화는 1도 올릴 때 사용하는 열이 많을수록, 열이 저장할 수 있는 mode가 많을수록 커짐
- 복합과정
Q) 부피가 0.500$dm^3$인 용기 속에 있는 25℃와 1.00bar의 아르곤 기체를 부피가 1.000$dm^3$가 될 때까지 팽창시키면서 함께 가열을 하여 온도를 100℃가 되게 하였을 때 엔트로피 변화는?
A) 이때 온도와 부피가 모두 변했음 하지만 엔트로피는 상태함수이기때문에 위의 과정을 두단계로 나눠서 계산하면 됨
1단계 : 0.500$dm^3$에서 1.000$dm^3$로 등온 팽창 시킬 때 엔트로피 변화
$\Delta S=nRln(\frac{1.000}{0.500})$
2단계 : 일정 부피 하에서 25℃에서 100℃가 되었을 때 엔트로피 변화
$\Delta S= nC_{V,m}ln\frac{T_f}{T_i}$ 이때 아르곤 기체이므로 $C_{V,m}=3/2R$
이를 계산하면 $\Delta S= 0.173JK^{-1}$
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 3-3 계를 주목할 때 (0) | 2024.09.12 |
|---|---|
| 【물리화학1】 3-2 엔트로피의 측정 (1) | 2024.09.09 |
| 【물리화학1】 3장 2법칙과 3법칙 (2) | 2024.09.07 |
| 【물리화학1】 2-5 단열 변화 (4) | 2024.09.07 |
| 【물리화학1】 2-4 상태 함수와 완전 미분 (0) | 2024.09.07 |