물질이 일으킬 수 있는 가장 간결한 물리적 상태 변화는 바로 상평형 그림으로 설명할 수 있음
이는 추후 5장 단순 혼합물의 기초가 됨
1. 상의 안정도
- 상의 수
물질의 상 = 화학적 조성+물리적 상태 균일
상의 수는 P로 나타냄
- 상 전이
상 전이는 균질한 물질이 어떤 온도나 압력에 의해 하나의 상에서 다른 상으로 급격하게 변화하는 현상
전이 온도 $T_{trs}$ = 두 상이 평형을 이루는 온도
* 이때 두 상은 평형을 이루며 이때의 온도는 주어진 압력 하에서 Gibbs 에너지가 최소가 되는 온도임
# 상 전이를 확인하는 방법
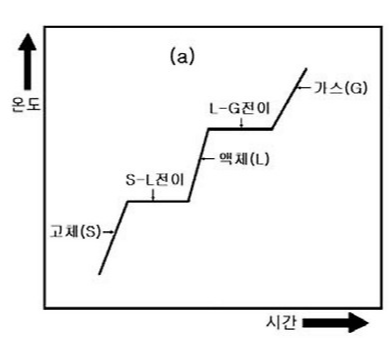
열법 분석과 시차 주사식 열 계량법은 전이가 일어나는 동안에는 시료에 열이 공급되거나 제거되는데도 온도가 변하지 않음을 이용
X선 회절 또한 고체에서의 상 전이를 확인하기 간편한데, 전이 온도 양쪽에서 상이한 회절 무늬가 관측됨
# 준안전 상
다이아몬드와 흑연은 탄소 동소체임, 이때 다이아몬드 Gibbs 에너지 > 흑연 Gibbs 에너지 임
하지만 매우 높은 온도가 아닌 이상 고체인 다이아몬드에서 고체인 흑연으로 변화는 과정은 측정이 거의 불가능함
즉, 열역학적으로 불안정하지만, 속도의 문제를 통해 전이를 일으키지 못하고 있는 상을 준안전 상이라고 함
* 열역학적으로는 자발적 과정이 맞음
- 상 안정도의 열역학적 기준
1성분 계에 대해서는 몰 Gibbs 에너지 $G_m=\mu$
이러한 화학 퍼텐셜 $\mu$는 계에서 변화를 일어나게 할 수 있는 잠재력, 즉 퍼텐셜의 척도가 됨
평형 상태에서는 한 물질이 몇 개의 상을 이루든 시료 전체를 통해서 화학 퍼텐셜이 균일해야 함
$dG=-SdT+Vdp$식에 화학 퍼텐셜을 적용하면 다음과 같음
$dG=-SdT+Vdp+\mu_1 dn_1+\mu_2 dn_2+...$
즉 등온 등압일 경우 $dG=\sum_{i=1}^n {\mu_i dn_i}$
이때 한 위치에서 화학 퍼텐셜이 $\mu_1$이고 다른 한 곳에서는 $\mu_2$일때 한 위치로부터 다른 위치로 dn만큼의 물질량이 이동되는 경우 계의 Gibbs 에너지는 각각 $-\mu_1 dn$과 $+\mu_2 dn$ 변해 전체 변화량 $dG=(\mu_2-\mu_1)dn$
이때 $\mu_2=\mu_1$일 경우에만 G가 변하지 않으며 이런 경우에만 계가 평형을 이루는 것임
2. 상 경계
한 물질의 여러 상들이 열역학적으로 안정하게 존재할 수 있는, 즉 Gibbs 에너지가 최소로 되는 영역의 그림이 상평형 그림임
이때 영역들 사이의 선을 상 경계라고 함
- 상 전이와 관련되는 특성들
증기 압력 : 증기 압력 또는 증기압은 증기가 고체 또는 액체와 동적 평형 상태에 있을 때 증기의 압력
온도가 높아질수록 이웃 분자로부터 멀리 떨어져 나갈 수 있는 분자가 많아져 증기 압력도 증가함
끓음(boiling) : 물의 표면뿐만 아니라 물속에서 물이 수증기로 상태가 변하는 현상
끓는점 : 액체의 증기압력이 외부 압력과 같아지는 온도
정상 끓는점 $T_b$ : 외부 압력이 1atm일 때의 끓는 온도
표준 끓는점 : 표준 압력을 1atm에서 1bar로 바꿨을 때의 끓는 온도, 1.00bar=0.987atm으로 표준 끓는점 < 정상 끓는점
밀폐된 용기 안에서 액체를 가열하면 액체는 끓지 않음, 그 이유는 온도가 올라감에 따라 액체가 기화하여 증기 압력(=증기 밀도)이 증가하기때문임
임계점 : 액체와 기체의 상의 구분이 사라지는 압력과 온도의 점
* 밀폐된 용기에서 계속 액체를 가열을 하면 증기의 밀도는 증가하고 액체의 밀도는 약간 감소하다 서로 같아지게 되고, 두 상 사이의 표면이 없어짐
* 이러한 상을 초임계 유체라고 함
임계 온도 $T_c$ : 임계점에서의 온도
임계 압력 $p_c$ : 임계점에서의 압력
녹는점 : 주어진 압력 하에서 액체상과 고체상이 평형을 이루면서 공존하는 온도
고체가 액체로 바뀌는 온도 = 액체가 고체로 바뀌는 온도이므로
녹는점 = 어는점
정상 어는점, 정상 녹는점 $T_f$ : 압력이 1bar에서의 어는점, 녹는점
* 정상 어는점, 녹는점과 표준 어는점, 녹는점의 차이는 무시할 수 있음
삼중점 $T_3$ : 해당 물질의 세 가지 상(기체, 액체, 고체)이 열역학적 평형 상태로 공존하는 온도와 압력
* 삼중점은 액체 상이 존재할 수 있는 최저 압력, 고체-액체 상 경계의 기울기가 오른쪽으로 기울어 질때(일반적)는 삼중점이 액체가 존재할 수 있는 최저 온도를 나타냄
* 물의 경우 고체-액체 상 경계의 기울기가 왼쪽으로 기울어져 있어 삼중점인 0.01℃보다 낮은 온도에서도 액체가 존재함
- 상의 규칙
상의 규칙은 평형을 이루는 상의 수를 변화시키지 않으면서 독립적으로 변화시킬 수 있는 변수의 수를 나타냄
$F=C-P+2$ 상 규칙
F는 자유도, C는 성분의 수, P는 상의 수
C, Component : 성분, 화학적으로 독립적인 계의 성분
* chemically independent constituent of the system
S, Constituent : 조성, 시스템에 있는 화학종
* chemical species present in the system
R, relation : 관계, 평형과 전하균형 등의 관계
$C=S-R$
이때 단일 성분 계의 경우 상 규칙에서 $C=1$이므로 $F=3-P$
단일 성분 계에서 $P=1$이라면 $F=2$가 되어 2변수 계 또는 2개의 자유도를 갖는 계라고 하며
$P=2$이라면 $F=1$이 되어 자유도가 1이됨
3. 세 가지 대표적 상평형 그림
- 이산화탄소
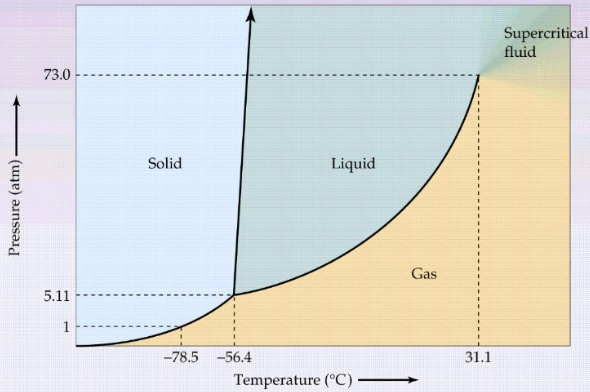
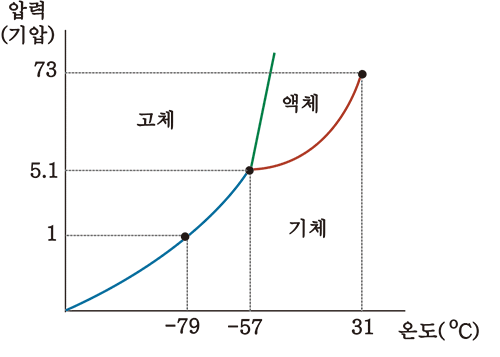
이산화탄소의 상 평형 그림을 보면, 고체-액체 경계선의 기울기가 양의 값임
* 즉, 녹는점과 어는점이 압력이 높아질수록 높아짐
대부분의 물질이 이러하며 예외로 물의 경우에는 기울기가 음임
또한 삼중점이 5.1atm으로 1atm보다 위에 있기에 정상적인 대기압 하에서는 이산화탄소는 액체로 존재할 수 없으며 고체의 이산화 탄소(드라이아이스)를 상온에 두면 기체로 승화함
- 물
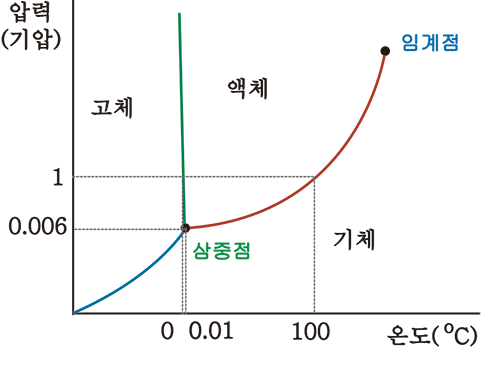
물의 경우 위에서 설명한 것처럼 고체-액체 경계선의 기울기가 음임
이러한 이유는 $V_m(ice)>V_m(water)$이기 때문인데, 수소결합에 의해 얼음의 몰부피가 물의 몰부피보다 크기 때문임
* 특정구간에서 고체의 Gibbs 에너지 < 액체의 Gibbs 에너지로 고체 상태가 더 안정함
따라서 삼중점을 기준으로 압력이 증가할때 물질의 밀도가 커지고(분자 사이의 거리가 가까워짐) 물질의 상태가 일반적으로는 기체-액체-고체 순으로 변하게 되는 것과 달리 물의 경우 기체-고체-액체 순으로 물의 상이 변함
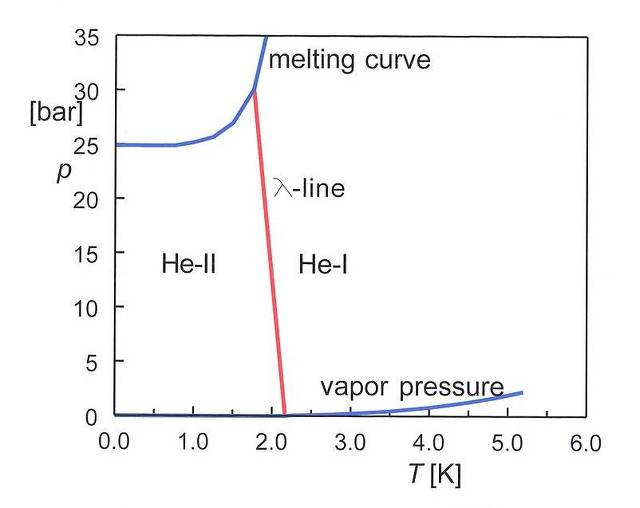
- 헬륨
헬륨은 원자의 질량이 매우 낮고 전자 수가 작아 이웃 원자간의 상호작용이 매우 약함
따라서 낮은 온도에서 비정상적인 성질을 지니는데, 온도가 아무리 낮아도 고체상과 기체상이 평형을 이루지 못함
* 헬륨이 매우 가볍기에 매우 낮은 온도에서도 큰 진폭을 갖고 진동하여 고체로 머물 수 없기 때문임
또한 헬륨-4는 두가지 액체상을 갖는데, 정상적인 액체상인 He-l부분과 초유체인 He-ll부분으로 나뉨
* He-ll의 경우 점성을 나타내지 않고 흐름
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5장 단순 혼합물 (0) | 2024.09.15 |
|---|---|
| 【물리화학1】 4-2 상 전이의 열역학적 양상 (0) | 2024.09.15 |
| 【물리화학1】 4장 순수한 물질의 물리적 변환 (0) | 2024.09.15 |
| 【물리화학1】 3-4 1법칙과 2법칙의 결합 (4) | 2024.09.13 |
| 【물리화학1】 3-3 계를 주목할 때 (0) | 2024.09.12 |