0. 이전 이야기
이전 포스팅에서는 상 전이와 상 평형을 나타내는 상 평형 그림에 대해 포스팅 하였음
상 전이는 균질한 물질이 어떤 온도나 압력에 의해 하나의 상에서 다른 상으로 급격하게 변화하는 현상을 말하는데, 이때 두 상은 평형을 이루며 이때의 온도는 주어진 압력 하에서 Gibbs 에너지가 최소로 되는 온도임
*이때 두 상의 퍼텐셜에너지는 같음
상 규칙은 물질의 자유도를 구하는 식으로 $F=C-P+2$이며 이때 F는 자유도, C는 성분의 수, P는 상의 수를 말함
단일 성분 계라면 $C=1$이므로 $F=3-P$
그리고 대표적인 이산화탄소, 물, 헬륨의 상 평형 그림에 대해 설명하였는데, 대부분의 물질은 고체-액체 경계의 기울기가 양수인 반면, 물의 경우 고체-액체 경계의 기울기가 음수임
* 이는 수소결합에 의해 얼음의 몰 부피가 물의 몰 부피보다 크기때문임
https://nate0707.tistory.com/83
【물리화학1】 4-1 순수한 물질의 상평형 그림
물질이 일으킬 수 있는 가장 간결한 물리적 상태 변화는 바로 상평형 그림으로 설명할 수 있음이는 추후 5장 단순 혼합물의 기초가 됨 1. 상의 안정도 - 상의 수 물질의 상 = 화학적 조성+물리적
nate0707.tistory.com
1성분 계에서 상의 화학 퍼텐셜 = 몰 Gibbs 에너지, $\mu$ = $G_m$
$dG=Vdp-SdT$이므로 압력과 온도에 따라 화학 퍼텐셜이 변화해 상 평형도 바뀜
이번 4-2장에서는 이러한 상 평형의 변화에 대해 정리할 것임
1. 안정도에 영향을 주는 조건
- 상의 안정도의 온도 의존
Gibbs 에너지의 온도 의존도는 다음과 같음
$(\frac{\partial G}{\partial T})_p=-S$
$(\frac{\partial \mu}{\partial T})_p=-S_m$ 화학 퍼텐셜의 T에 따른 변화
모든 물질의 $S_m>0$이므로 $\mu$의 T에대한 그래프의 기울기는 음수
또한 $S_m(g)>S_m(l)>S_m(s)$이므로 $\mu$의 온도에 대한 기울기는 기체-액체-고체 순으로 가파름
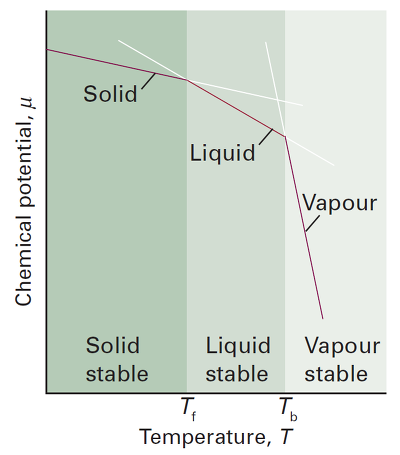
그래프를 그린 후 주어진 상에서 $\mu$가 최소인 상이 그 온도에서 가장 안정한 상임
- 녹는점에 미치는 압력의 영향
Gibbs 에너지의 압력 의존도는 다음과 같음
$(\frac{\partial G}{\partial p})_T=V$
$(\frac{\partial \mu}{\partial p})_T=V_m$ 화학 퍼텐셜의 V에 따른 변화
모든 물질의 $V_m>0$이므로 $\mu$의 V에대한 그래프의 기울기는 양수
또한 $V_m(g)>V_m(l)>V_m(s)$이므로 $\mu$의 부피에 대한 기울기는 기체-액체-고체 순으로 가파름
그러나 물의 경우 $V_m(g)>V_m(s)>V_m(l)$이므로 압력을 높여 주면 고체의 화학 퍼텐셜이 액체의 것보다 많이 증가함
* 이는 수소결합때문에 얼음이 특별한 구조를 구성하기 때문임
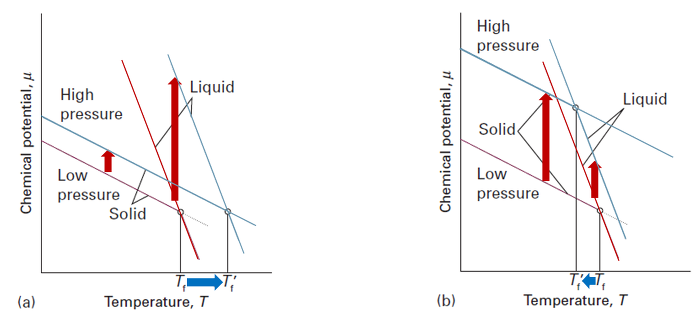
(a) : 일반적인 물질의 경우 $V_m(l)>V_m(s)$이므로 $\mu(l)$가 $\mu(s)$보다 많이 증가함
따라서 이들의 교점인 녹는점의 온도도 증가함
(b) : 물의 경우 $V_m(s)>V_m(l)$이므로 $\mu(s)$가 $\mu(l)$보다 많이 증가함
따라서 이들의 교점인 녹는점의 온도는 감소함
- 증기 압력에 미치는 외부 압력의 영향
응축 상에 압력을 가하면 그 증기 압력이 올라감
* 응축 상으로부터 분자가 기체상 속으로 짜내어져 들어가기 때문
부분 증기 압력 : 비활설 기체를 이용하여 응축 상에 압력을 가할 때 응축 상과 평형을 이루고 있는 증기의 부분 압력
이때 다음과 같은 식이 성립함
$p=p^*e^{V_m(l) \Delta P/RT}$ 가해준 압력 $\Delta P$가 증기압력 p에 미치는 영향
<증명>
평형에서 액체와 증기의 화학 퍼텐셜이 같아야 함, 즉 $\mu(l)=\mu(g)$
평형을 깨뜨리지 않는 변화에 대해 각각의 화학 퍼텐셜의 변화량이 같아야함 $d \mu(l)=d \mu(g)$
액체의 압력 P가 dP만큼 변화하고 기체의 압력 p가 dp만큼 변화했다고 한다면 $d\mu(l)=V_m (l)dP$ $d \mu(g)=V_m (g)dp$
$V_m(g)=RT/p$이므로 위의 두식을 연립하면 $\frac{RTdp}{p}=V_m(l)dP$
여기서 적분 구간만 구하면 위 식을 계산할 수 있음
액체의 압력 P = 여분의 압력이 작용하지 않을 때 정상 증기 압력 $p^*$
액체에 $\Delta P$만큼의 압력이 여분으로 작용했을 때 $P=p+ \Delta p=p^*+ \Delta P$
따라서 위의 구간에 따라서 $\frac{RTdp}{p}=V_m(l)dP$를 적분하면
$\int_{p^*}^p \frac{dp}{p}= \frac{1}{RT} \int_{p^*}^{p^*+\Delta P} V_m (l)dP$ $=\frac{V_m(l)}{RT} \int_{p^*}^{p^*+\Delta P} dP$ $= ln \frac{p}{p^*}= \frac{V_m(l)}{RT} \Delta P$
$p=p^*e^{V_m(l) \Delta P/RT}$를 구할 수 있음
2. 상 경계의 위치
두 상이 평형을 이룰때 이들의 화학 퍼텐셜이 같아야 함
즉, $\mu(\alpha; p,T)=\mu(\beta; p,T)$
이 식을 풀어 p를 T에 대한 함수로 나타내면 경계선을 나타내는 식을 구할 수 있음
- 상 경계선의 기울기
상 경계선의 기울기를 구하기 위해서는 dp/dT를 구해야 함
우선 이 경우에 $d\mu(\alpha)=d\mu(\beta)$이고 $dG=d/mu=Vdp-SdT$이므로
$-S_m(\alpha)dT+V_m(\alpha)dp=-S_m(\beta)dT+V_m(\beta)dp$
${S_m(\beta)-S_m(\alpha)}dT={V_m(\beta)-V_m(\alpha)}dp$
$S_m(\beta)-S_m(\alpha)=\Delta_{trs} S$
$V_m(\beta)-V_m(\alpha)=\Delta_{trs} V$
즉, $\Delta_{trs}dT=\Delta_{trs} VdpS$
$\frac{dp}{dT}=\frac{\Delta_{trs} S}{\Delta_{trs} V}$ Clapeyron 식
이 식은 상 경계선상의 임의의 점에서의 접선의 기울기를 나타내는 식
- 고체-액체 경계
고체가 액체로 녹을때 몰 엔탈피 변화 $\Delta_{fus} H$가 수반됨
$\frac{dp}{dT}=\frac{\Delta_{trs} S}{\Delta_{trs} V}$ Clapeyron 식에서 $\Delta_{trs} S=\frac{\Delta_{fus} H}{T}$를 이용하면
$\frac{dp}{dT}=\frac{\Delta_{fus} H}{T \Delta_{fus} V}$ 고체-액체 경계선의 기울기
용융 엔탈피 $\Delta_{fus} H$ 는 He-3을 제외하고 양수이며 $\Delta_{fus} V$도 대부분 양수이므로 상 경계선의 기울기도 양수
또한 매우 가파른 기울기를 갖음
$\Delta_{fus} H$와 $\Delta_{fus} V$가 압력과 온도에 거의 무관하다고 가정하고 고체-액체 경계선의 기울기 식을 적분하면
$p=p^*+\frac{\Delta_{fus} H}{\Delta_{fus} V}ln\frac{T}{T^*}$
$ln\frac{T}{T^*}=ln(1+\frac{T-T^*}{T} \approx \frac{T-T^*}{T}$
* $ln(1+x) \approx x$
$p=p^*+\frac{\Delta_{fus} H}{T^* \Delta_{fus} V}(T-T^*)$
- 액체-증기 경계
이것도 고체-액체 경계의 방식과 같음
$\frac{dp}{dT}=\frac{\Delta_{vap} H}{T \Delta_{vap} V}$ 액체-증기 경계선의 기울기
증발 엔탈피 $\Delta_{vap} H$는 양이며 $\Delta_{vap} V$ 또한 양이므로 dp/dT는 양이 됨
하지만 이는 고체-액체 경계선보다 훨씬 작고 그렇기에 dT/dp가 매우 큼, 즉 끓는점은 온도보다 압력에 더 크게 의존함
$\Delta_{vap} V=V_m(g)-V_m(l)$에서 $V_m(g)>>V_m(l)$이므로 $\Delta_{vap} V \approx V_m(g)$
$\frac{dp}{dT}=\frac{\Delta_{vap} H}{T V_m(g)}=\frac{\Delta_{vap} H}{T (RT/p)}=\frac{p \Delta_{vap} H}{RT^2}$
이때 dx/x=d lnx를 이용하면
$\frac{dlnp}{dT}=\frac{\Delta_{vap} H}{RT^2}$ Clausius-Clapeyron 식
이를 적분하면
$\int_{lnp^*}^{lnp} dlnp=\frac{\Delta_{vap} H}{R} \int_{T^*}^T \frac{dT}{T^2}=-\frac{\Delta_{vap} H}{R}(\frac{1}{T}-\frac{1}{T^*})$
이를 정리하면
$p=p^*e^{-\chi}$ $\chi=\frac{\Delta_{vap} H}{R}(\frac{1}{T}-\frac{1}{T^*})$
임계온도 이상에서는 액체상이 존재하지 않으므로 이 곡선은 임계 온도 $T_c$에서 끝남
- 고체-증기 경계
고체-증기 경계의 경우 액체-증기 경계에서와 완전히 같음
대신 $\Delta_{vap} H$대신 $\Delta_{sub} H$를 사용해야 하며
$\Delta_{sub} H=\Delta_{vap} H+\Delta_{fus} H$로 승화 엔탈피가 증발 엔탈피보다 크기 때문에 승화 곡선이 증발 곡선보다 더 가파른 기울기를 갖음
$\frac{dp}{dT}=\frac{\Delta_{sub} H}{T \Delta_{sub} V}$ 고체-증기 경계선의 기울기
3. Ehrenfest의 상 전이 분류
- 열역학적 근거
상전이가 일어나는 시점에 화학 퍼텐셜의 미분 중 불연속적인 양이 생기는데 여기서 몇번 미분을 해야 이런 양이 나타나는가가 분류의 기준이 됨
$(\frac{\partial \mu (\beta}{\partial p})_T-(\frac{\partial \mu (\alpha}{\partial p})_T=V_m(\beta)-V_m(\alpha)=\Delta_{trs} V$
$(\frac{\partial \mu (\beta}{\partial T})_p-(\frac{\partial \mu (\alpha}{\partial T})_p=-S_m(\beta)+S_m(\alpha)=-\Delta_{trs} S=-\frac{\Delta_{trs} H}{T_{trs}}$
용융이나 증발 과정에서 $\Delta_{trs} V$와 $\Delta_{trs} S$가 0아니므로
화학 퍼텐셜을 압력이나 온도에 대해 그릴 경우 전이를 전후로 기울기가 달라짐
1차 상전이는 화학 퍼텐셜의 온도에 관한 1차 도함수가 불연속이 되는 전이를 말함
다양한 고체,액체,기체전이가 여기에 속함
2차 상전이는 화학 퍼텐셜을 두 번 미분한 양이 비연속적인 경우임
철과 같은 물질의 강자기 상전이를 포함
- 분자 수준의 해석
1차 전이가 일어날 때는 원자, 분자 또는 이온의 재배치가 일어나서 이들의 상호작용 에너지가 변함
예를들어 증발이 일어나면 분자들 사이의 인력이 제거되며 이온결합시 이온의 재배치가 일어남
2차 상 전이 중에는 고체 결정 구조의 대칭 변화가 생김
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 5-1 혼합물에 대한 열역학 (0) | 2024.09.17 |
|---|---|
| 【물리화학1】 5장 단순 혼합물 (0) | 2024.09.15 |
| 【물리화학1】 4-1 순수한 물질의 상평형 그림 (0) | 2024.09.15 |
| 【물리화학1】 4장 순수한 물질의 물리적 변환 (0) | 2024.09.15 |
| 【물리화학1】 3-4 1법칙과 2법칙의 결합 (4) | 2024.09.13 |