0. 이전 이야기
저번 포스팅에서는 표준 엔탈피에 대하여 포스팅함
엔탈피란 일정 압력에서의 열의 변화를 설명하는 개념인데
이때 1bar의 압력하의 표준 상태에서의 변화인 표준 엔탈피를 많이 이용함
표준 엔탈피는 상태함수이기에 여러 성질을 갖는데 그 중 하나가 Hess의 법칙이 성립하는 것임
* Hess의 법칙이란 한 반응을 일련의 여러 반응 성분으로 분해했을 때, 이들 성분 반응들의 표준 반응 엔탈피를 합하면 전체의 표준 반응 엔탈피가 된다는 것임
또한 화학식으로부터 구할 수 있는 반응 엔탈피의 변화는 물질들의 열 용량에 의존함
https://nate0707.tistory.com/73
【물리화학1】 2-3 열화학
저번 포스팅에서는 엔탈피에 대해서 학습함엔탈피란 일정한 압력하에서 열의 변화를 설명하기 위핸 개념등압과정에서 열의 변화 ≠ 내부에너지 변화 이므로 새로운 정의를 한 것 이전 글https:/
nate0707.tistory.com
# 상태함수와 경로함수
상태함수 state function : 계의 현재 상태에만 의존하고 과거에 어떤 일이 있었는지는 무관함
* 내부 에너지와 엔탈피 등은 상태함수임
경로함수 path function : 두 상태들 사이의 경로에 의존하는 물리적 성질
* 일과 열 등은 경로함수임
엔탈피와 내부 에너지는 상태함수이기 때문에 이를 조작해 열용량들 사이의 관계와 기체를 냉각시키는데 이용되는 Joule-Thomson 효과를 유도할 수 있음
1. 완전 미분과 불완전 미분
완전 미분(exact differential) : 일반적으로 어떤 한 미분을 적분한 결과가 그 처음과 최종 상태 사이의 적분 경로에 무관한 경우
$\Delta U= \int_i^f{dU}$
$\Delta U$ 값읜 처음과 마지막 상태에만 의존하고 경로에 무관함
불완전 미분(inexact differential) : 적분 결과가 처음과 최종 상태 사이의 경로에 의존하는 무한소량
$q=\int_{i,path}^f{dq}$
q는 상태 함수가 아니므로 열로서 가해진 에너지를 $q_f-q_i$와 같이 나타낼 수 없어 $\Delta q$라고 사용하지 않음
2. 내부 에너지의 변화
조성이 고정된 닫힌계에서, $U=f(V,T,p)$
이때 상태방정식 $pV=nRT$를 이용해 U를 두가지 독립 변수로 나타낼 수 있음
이때 주로 $U=f(V,T)$를 이용함
- 일반적 고찰
이변수 함수일 때 $z=f(x,y)$일 때 z의 변화량은 다음과 같음
$dz=(\frac{\partial z}{\partial x})dx$ $(\frac{\partial z}{\partial y})dy$
이를 이용하여 T와 V에 따른 U의 변화를 나타내는 일반식은 다음과 같음
$dU=(\frac{\partial U}{\partial V})_TdV+(\frac{\partial U}{\partial T})_VdT$
여기서 dV와 dT의 비례 상수들은 각각 의미를 가지고 있음
dT의 비례상수인 $(\frac{\partial U}{\partial T})_V$는 일정-부피 열용량 $C_V$이고
dV의 비례상수인 $(\frac{\partial U}{\partial V})_T$는 한 물질의 내부 에너지가 일정 온도에서 그 부피에 어떻게 의존하는지를 나타내는 $\pi_T$ 임
* $\pi_T$는 압력과 동일한 단위를 갖지만, 시료 안의 분자들 사이의 상호작용 때문에 생기는 것이며 이 때문에 내부적 압력이라고 부름
따라서 정리하면
$dU=\pi _TdV+C_VdT$
* 일반적으로 등온과정에서 내부에너지 변화가 0이라고 알고있지만, 이는 이상기체일 경우에만 적용됨
# 기체의 종류에 따른 내부적 압력 변화
내부적 압력은 분자 사이의 상호작용에 의해 생기는 것이기에 분자들 사이의 상호작용이 없는 완전 기체는 $\pi_T=0$
van der Waals 상태식을 따르는 기체의 경우 인력 지배적인 경우 부피가 증가시 퍼텐셜 에너지가 증가하여 내부에너지도 증가함
반발력이 지배적일 경우 부피가 팽창하면 입자 간 거리가 멀어지고 퍼텐셜 에너지가 감소하여 내부에너지가 감소함
이상 기체(ideal gas) : $\pi _T=0$
인력이 지배적인 기체(attraction-dominant gas) : $\pi _T>0$
반발력이 지배적인 기체(repulsion-dominant gas) : $\pi _T<0$

# 기체가 등온 팽창할 때의 내부 에너지 변화 측정 실험
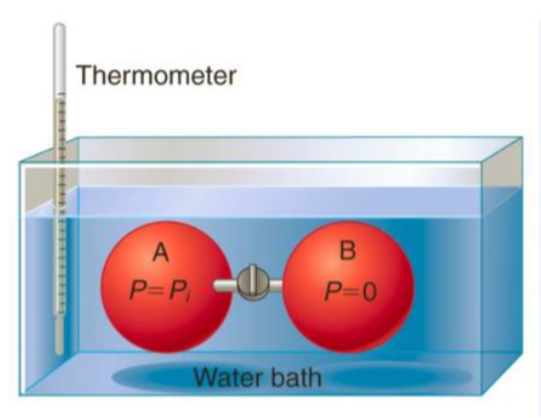
James Joule은 기체를 진공 속에서 팽창시킬 때 생기는 온도 변화를 측정함으로써 $\pi _T$를 측정하려함
우선 A에서 B로 진공 속으로 팽창되었으므로 아무런 일이 행해지지 않음 $w=0$
또한 물의 온도가 변하지 않았으므로 $q=0$
따라서 이 실험에서는 $\Delta U=0$
하지만 실제로는 이 장치의 열용량이 매우 크기에(많은 열을 가해도 온도를 올리기 어려움) 제대로된 온도 측정이 안됨
- 일정 압력 하에서의 내부 에너지 변화
실제 상황에서는 압력이 일정한 경우가 상당히 많이 사용됨
$dU=\pi _TdV+C_VdT$ 이 식에서 양변을 dT로 나눈 후 일정 압력의 조건을 부과하면
$(\frac{\partial U}{\partial T} )_p=\pi_T ( \frac{ \partial V}{ \partial T} )_P+C_V$
이때 이미 알고있는 물리적 양들이 존재함
팽창 계수는 온도 상승에 수반되는 부피의 부분 변화율로
$α= \frac{1}{V}( \frac{ \partial V}{ \partial T} )_p$
등온 압축도는 압력을 조금 높였을 때의 부피의 부분 변화율로
$k_T=- \frac{1}{V} ( \frac{ \partial V}{ \partial p} )_t$
* 이 식에 부호 -가 있는 이유는 압력이 증가하여 dp가 양수일 때 dV는 음수이므로 이 값을 양수로 만들기 위함임
팽창 계수 α를 이용하여 맨 위의 식을 다시 작성하면
$( \frac{ \partial U}{ \partial T} )_p= α \pi_TV+C_V$
완전 기체에 대해서 $ \pi_T=0$ 이므로
$( \frac{ \partial U}{ \partial T} )_p=C_V$
원래는 $( \frac{ \partial U}{ \partial T} )_v=C_V$이지만 이상기체의 경우 내부에너지는 온도의 함수이므로 p,V는 상관이 없음
따라서 이를 통해 $C_p$와 $C_V$ 사이의 관계를 구할 수 있음
$C_p-C_V= $ $( \frac{ \partial H}{ \partial T} )_p - ( \frac{ \partial U}{ \partial T} )_p$
$H=U+pV=U+nRT$
$C_p-C_V= ( \frac{ \partial (U+nRT)}{ \partial T} )_p - ( \frac{ \partial U}{ \partial T} )_p=nR$
이상 기체뿐 아닌 보편적으로는 다음과 같은 관계를 갖음
$C_p-C_V= \frac{α^2TV}{k_T}$
3. Joule-Thomson 효과
엔탈피 $H=U+pV$이고 U,p,V 모두 상태함수이므로 H도 상태함수임
또한 phase rule에 의해 $H=f(p,T)$로 나타낼 수 있음
$dH=( \frac{ \partial H}{ \partial p} )_Tdp+ ( \frac{ \partial H}{ \partial T} )_pdT$
이때 둘째 편도함수 $( \frac{ \partial H}{ \partial T} )_p=C_p$이고
만일 엔탈피가 변하지 않는다면 dH=0이고
$(\frac{\partial H}{\partial p})_Tdp$ $=-C_p dT$ 일정 H에서
양변을 dp로 나눠주면
$(\frac{\partial H}{\partial p})_T$ $=-C_p(\frac{\partial T}{\partial p})_H$ $=-C_p \mu$
* 앞으로 다룰 Joule-Thomson 계수는 위의 첫째 편도함수를 구하기 위한 과정임
Joule-Thomson 계수$\mu$는 다음과 같음
$\mu =(\frac{\partial T}{\partial p})_H$
이 관계는 일정-압력 열용량과 부피를 연관시키는데 유용하게 쓰이며 기체의 액화를 논할때도 쓰임
- Joule-Thomson 효과의 관찰
Joule과 William Thomson은 등-엔탈피 과정을 발생시켜 실험을 진행함
기체는 분출구 역할을 하는 다공성 칸막이를 통해 팽창되고, 전체 장치가 단열화 되어있음
실험 결과 압력이 낮아진 쪽의 온도가 더 낮고, 그 온도차는 팽창 전후의 압력차에 비례한다는 것을 발견함
# 등온 Joule-Thomson 계수
현대에는 간접적으로$\mu$를 측정 등엔탈피 과정은 측정하기 힘들기에 등온과정으로 측정
열교환기를 통해 온도를 필요한 대로 맞춘 기체를 일정 압력으로 계속 주입시키면서 다공성 플러그를 통해 단열 용기 속으로 보냄
이때 급격한 압력 강하를 측정하고 이로인해 생기는 냉각효과는 전열기로 상쇄시켜주며 공급되는 에너지를 측정함
이를 통해 $\Delta H/ \Delta p$의 값을 통해 $\mu_T$를 구하고 $\mu$값도 구함
$\mu_T=(\frac{\partial H}{\partial p})_T=-C_p\mu$ by Euler chain reaction
# 기체의 종류에 따른 줄톰슨 계수 $\mu$
이상기체에서 엔탈피가 일정 = 온도 변화 없음이기에 줄톰슨 계수가 0이됨
이상 기체(ideal gas) : $\mu _T=0$
인력이 지배적인 기체(attraction-dominant gas) : $\mu _T>0$
반발력이 지배적인 기체(repulsion-dominant gas) : $\mu _T<0$
* 어느 한 온도에서 팽창될 때 가열효과를 나타내는 기체는 그 온도를 높은 반전 온도 $T_1$ 이하로 내려 주면 냉각 효과를 나타냄
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 3장 2법칙과 3법칙 (2) | 2024.09.07 |
|---|---|
| 【물리화학1】 2-5 단열 변화 (4) | 2024.09.07 |
| 【물리화학1】 2-3 열화학 (0) | 2024.09.05 |
| 【물리화학1】 2-2 엔탈피 (8) | 2024.09.04 |
| 【물리화학1】 2-1 내부 에너지 (5) | 2024.09.03 |