열역학 제 1법칙 : 고립계의 총 에너지는 일정하다
1. 일, 열, 및 에너지
- 기초 정의
# 계와 주위
계 (system) : 우리가 관심을 갖는 부분
주위 (surrounding) : 계 밖의 나머지 부분
# 여러가지 계
열린 계 (open system) : 주위와 에너지 및 물질이 출입할 수 있는 계
닫힌 계 (closed system) : 주위와 에너지는 교환할 수 있지만 물질은 출입할 수 없는 계
고립 계 (isolated system) : 주위와 에너지와 물질 모두 출입할 수 없는 계

# 일, 열, 에너지
일 (Work) : 대립하는 힘(opposing force)에 맞서는 운동
에너지 (energy) : 그 계가 할 수 있는 일의 능력(capacity to do work)
열 : 한 계에서 다른 계로 에너지가 이동하는 방법 중, 일 또는 물질의 직접 이동이 아닌 방법
# 열 관련 용어
투열성(diabatic) : 에너지를 열로 이전시킬 수 있는 경계
단열성(adiabatic) : 에너지를 열로 이전시키지 못하는 경계
발열 과정(exothermic process) : 에너지를 주위에다 열로서 방출하는 과정
흡열 과정(endothermic process) : 주위로부터 에너지를 흡수하는 과정
- 열과 일의 분자 수준 해석
열운동 = 분자들의 무질서한(disordely) 운동 → 찬 계의 분자를 자극해 더 활발하게 움직이게 하여 에너지를 증가시킴
ex) 계가 주위를 가열할 때는 계의 분자들이 주위 분자들의 열운동을 활발하게 함
일 = 조직적(organized) 운동
ex) 계가 일을 할 때는 주위에 있는 원자나 전자들을 조직화된 방식으로 이동케 함
ex) 계에 일이 행해질 때는 조직화된 방식으로 에너지가 계에 이전됨
# 일과 열의 구분 → 주위에서 결정됨
일 = 주위에 있는 원자들의 조직적인 운동을 이용하는 에너지
열 = 주위의 열운동을 이용하는 에너지
2. 내부 에너지(internal energy, U)의 정의
내부 에너지(internal enegy) = 계(system) 전체 E
U = 계의 성분 알맹이의 운동에너지(kinetic energy) + 위치에너지(potential enegy)
* 계의 전체적인 운동에 기인되는 것과 같은 운동에너지는 포함하지 않음 (지구의 회전 등)
내부 에너지 변화는 다음과 같이 나타냄
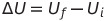
내부 에너지는 계의 현재 상태에만 의존하고 그 상태가 어떻게 이루어졌는가에 대해서는 무관한 상태 함수(state function)
* 상태함수의 반대는 경로함수(path function)으로 그 상태가 어떻게 이루어 졌는가에 의해 달라짐
- 내부 에너지의 분자 수준 해석
# 분자들의 세가지 운동 방식, (= 분자들이 가질 수 있는 자유도, mode 수)
병진 운동(translation) : 공간 속에서의 질량 중심의 이동
질량 중심 주위의 회전(rotation)
진동(vibration) : 질량 중심은 이동하지 않은 채로 결합 길이와 결합 각의 변화
* 이 셋 중 병진 운동과 회전에 의한 운동만 온도에 비례하는 기여를 하며 내부 에너지에 영향을 줌
분자의 물리적 성질이나 화학적 성질은 대부분 이 운동 방식들이 갖는 에너지에 의존함
# 단원자 분자, 다원자 분자의 내부 에너지
기체 분자의 병진 운동(translation)에 의해 기인되는 평균 에너지는 3/2kT
*k와 아보가드로수 Na를 곱하면 기체상수 R이 됨, kNa=R
단원자 분자(monatomic gas) : Um(0)+3/2RT
* 병진 운동에 의한 에너지 3/2RT
선형 다원자 분자(linear polyatomic gas) : Um(0)+3/2RT+RT
* 병진 운동에 의한 에너지 3/2RT + 회전에 의한 에너지 RT, 이때 선형이기 때문에 x,y,z축 중 2개의 자유도를 가짐
비선형 다원자 분자(nonlinear polyatmoic gas) : Um(0)+3/2RT+3/2RT
* 병진 운동에 의한 에너지 3/2RT + 회전에 의한 에너지 3/2RT, 이때 비선형이기 때문에 x,y,z축 3개 모두의 자유도를 가짐
# Um(0)은 무엇인가 ?
Um(0)는 T=0 일 때의 몰 내부 에너지
완전 기체 분자들일 경우 분자간 상호작용이 없으므로 분자들 사이의 거리가 에너지에 영향이 없음
즉 완전 기체의 내부 에너지는 기체가 차지하는 부피에 무관함, Um(0)=0
- 1법칙의 수식화
열역학의 1법칙 : 고립된 계의 내부 에너지는 일정함
이를 수식으로 나타내면 다음과 같음
$ \Delta U=q+w$
3. 팽창 일
변화의 양이 작을 때
$ \Delta U=q+w$
위의 식에서 상태의 미소 변화와 내부 에너지의 미소 변화를 주목하면 다음과 같은 식이 나옴
$dU=dq+dw$
- 일에 대한 일반적 식
팽창 일(expansion work = pv work)은 힘 F가 dz만큼의 거리를 이동했을 때 다음과 같이 정의됨
이때 (-) 부호는 다른 변화가 없다면 이 계의 내부 에너지가 감소된다는 사실을 나타낸 것임
$ dw=Fs=- |F| dz$
dz > 0 이면 dw는 음
dz < 0 이면 dw는 양
단면적을 A, 외부 압력을 Pex라 했을 때,
$F=p_{ex}A$
$ w=- \int_{V_i}^{V_f}{p_{ex}dV}$
Vf>Vi 이면 w는 음
Vf<Vi 이면 w는 양
- 일정 압력에서의 팽창
대기의 압력을 받는 피스톤 등의 과정을 생각해 보면
$ w=-{p_{ex}} \int_{V_i}^{V_f}{dV}=-p_{ex}(v_f-V_i)$
# 자유 팽창(zero opposing force)
자유 팽창이란 맞서는 대립 힘이 0일 때를 말함
즉 Pex=0이고 w=0임
- 가역 팽창(reversible expansion)
가역 변화란 변수를 미소하게 변화시켜서 그 변화를 역방향으로 일어나게 할 수 있는 과정을 말함
가역적 팽창을 일으키려면, 각 팽창 단계마다 외부압력 Pex와 내부압력 p를 같게 해주어야함
만약 외부압력과 내부압력이 크게 다를 경우 과정의 역방향이 일어나지 않는 비가역적 팽창이 일어남
가역 팽창 일은 다음과 같음
$dw=-p_{ex}dV=-pdV$
$w=- \int_{V_i}^{V_f}{pdV} $
여기서 p를 V의 함수로 나나태면 이 적분값을 계산할 수 있음
- 등온 가역 팽창
등온 가역 팽창은 위의 $w=- \int_{V_i}^{V_f}{pdV} $ 식에서 이상기체 방정식 $pV=nRT$ 를 이용함
$w=- nRT\int_{V_i}^{V_f}{ \frac{dV}{V} } =-nRTln \frac{V_f}{V_i} $
$V_f>V_i$ : w는 음수
* 계가 주위에 일을 하며 그만큼 계의 내부 에너지가 감소함
* 하지만 추후에 이를 보충하는 열에너지가 유입되어 전체적 U는 일정함
$V_f<V_i$ : w는 양수
또한 w는 T에관한 함수이기 때문에 같은 부피 변화라 하여도 높은 온도에서 일어날수록 더 많은 일이 행해짐
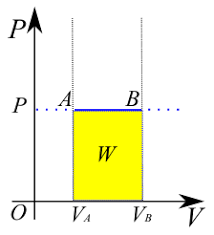
# 가역 과정과 비가역 과정의 한 일
위의 그래프에서
A+B : 등온가역 상태에서의 팽창과 수축이 일어날 때 한 일
B : 비가역적으로 팽창될때(v1에서 v2로) 한 일
팽창 시 각 단계에서 외부 압력을 내부 압력에 맞춰줌으로써 계는 미는 힘을 조금도 낭비시키지 않았기에 가역 과정이 비가역 과정보다 많은 일을 얻을 수 있음
* 비가역 수축일 경우(v2에서 v1으로) 한 일은 p1(v2-v1)에 해당하는 더 큰 직사각형의 넓이로 가역 과정보다 한 일이 많음
4. 열의 출입
일반적인 계의 내부 에너지 변화는 다음과 같음
$dU=dq+dw_{exp}+dw_e$
내부 에너지 변화 = 열의 변화 + 팽창일의 변화 + 비팽창일의 변화
이때 부피를 일정하게 해 준 계는 팽창일을 할 수 없으며 계가 다른 종류의 일도 할 수 없다면 dw=0이 됨
즉 위의 조건에서 다음이 성립함
$dU=dq$
이를 부피 V가 일정하다는 의미의 아래 첨자를 이용하면 다음과 같음
$dU=dq_V$
$ \Delta U=q_V$
- 열 계량
system마다 열에 대한 맷집이 다르기에 열 계량을 통해 이를 측정할 수 있음
물리적 혹은 화학적 변화가 일어날 때 열로서 이전되는 에너지를 조사하는 것이 열 계량임
보편적으로 $q_v$를 측정하는 데 쓰이는 장치는 단열 반응통 열량계임
열량계의 온도변화 $ \Delta T$는 반응에서 방출되거나 흡수되는 열에너지에 비례하며 이를 이용해 $q_v$와$ \Delta U$를 측정함
$q=C \Delta T$, 이때 C는 열량계 상수
$q=It \Delta \phi $, I는 전류 t는 시간, $\Delta \phi$는 전위차
두 식을 이용해 열량계 상수 C를 구할 수 있음
- 열용량
물질의 양에 따라서 열에 의해 증가하는 내부 에너지의 정도가 달라지므로 열용량을 구할 때는 주로 일정 부피 조건을 사용함
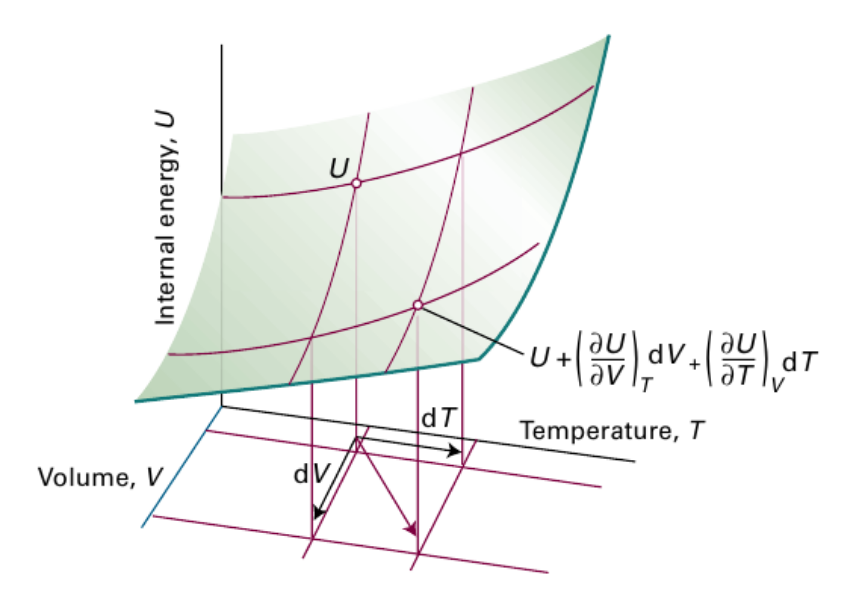
$C_V= \frac{ \Delta q_V}{ \Delta T} =( \frac{ \partial U}{ \partial T})_V $
* $C_V$가 크다는 것은 같은 열 $q_V$로 온도 변화가 작다는 것으로 온도를 올리기 어렵다는 말임
* 상전이 온도에서는 시료의 열용량이 무한대가 되며 아무리 많은 열을 가해 주어도 온도가 올라가지 않음
* 편도함수란 변수가 여러개일 때 하나를 고정 후 미분하는 것
* 여기서는 U,T,V의 함수에서 변수 V를 고정 후 U를 T에 대해 미분하여 열용량 C를 구함
# 열용량의 크기 성질과 세기 성질
열용량은 크기 성질(extensive)로 100g의 물은 1g의 물보다 100배의 열용량을 가짐
일정-부피 몰 열용량 $C_{V,m}=C_V/n$은 1mol 물질의 열용량이며 세기 성질(intensive)임
열용량은 일정부피 계의 내부 에너지 변화를 온도 변화와 연관시키는데 이용함
$dU=C_VdT$
이때 계산의 편의를 위해 $C_V$를 상수 취급하면 다음 식이 나옴
$ \Delta U=C_V \Delta T$
위의 관계식을 이용하면 시료의 열용량을 간단하게 측정할 수 있음
일정량의 열을 시료에 가하고 여기에 기인되는 온도 상승을 나눠주면 시료의 일정-부피 열용량이 나옴
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 2-3 열화학 (0) | 2024.09.05 |
|---|---|
| 【물리화학1】 2-2 엔탈피 (8) | 2024.09.04 |
| 【물리화학1】 2장 열역학 제 1법칙 (2) | 2024.09.03 |
| 【물리화학1】 1장 기체의 성질 목차 (0) | 2024.08.09 |
| 【물리화학1】 1-3 실제 기체 (0) | 2024.08.09 |
열역학 제 1법칙 : 고립계의 총 에너지는 일정하다
1. 일, 열, 및 에너지
- 기초 정의
# 계와 주위
계 (system) : 우리가 관심을 갖는 부분
주위 (surrounding) : 계 밖의 나머지 부분
# 여러가지 계
열린 계 (open system) : 주위와 에너지 및 물질이 출입할 수 있는 계
닫힌 계 (closed system) : 주위와 에너지는 교환할 수 있지만 물질은 출입할 수 없는 계
고립 계 (isolated system) : 주위와 에너지와 물질 모두 출입할 수 없는 계

# 일, 열, 에너지
일 (Work) : 대립하는 힘(opposing force)에 맞서는 운동
에너지 (energy) : 그 계가 할 수 있는 일의 능력(capacity to do work)
열 : 한 계에서 다른 계로 에너지가 이동하는 방법 중, 일 또는 물질의 직접 이동이 아닌 방법
# 열 관련 용어
투열성(diabatic) : 에너지를 열로 이전시킬 수 있는 경계
단열성(adiabatic) : 에너지를 열로 이전시키지 못하는 경계
발열 과정(exothermic process) : 에너지를 주위에다 열로서 방출하는 과정
흡열 과정(endothermic process) : 주위로부터 에너지를 흡수하는 과정
- 열과 일의 분자 수준 해석
열운동 = 분자들의 무질서한(disordely) 운동 → 찬 계의 분자를 자극해 더 활발하게 움직이게 하여 에너지를 증가시킴
ex) 계가 주위를 가열할 때는 계의 분자들이 주위 분자들의 열운동을 활발하게 함
일 = 조직적(organized) 운동
ex) 계가 일을 할 때는 주위에 있는 원자나 전자들을 조직화된 방식으로 이동케 함
ex) 계에 일이 행해질 때는 조직화된 방식으로 에너지가 계에 이전됨
# 일과 열의 구분 → 주위에서 결정됨
일 = 주위에 있는 원자들의 조직적인 운동을 이용하는 에너지
열 = 주위의 열운동을 이용하는 에너지
2. 내부 에너지(internal energy, U)의 정의
내부 에너지(internal enegy) = 계(system) 전체 E
U = 계의 성분 알맹이의 운동에너지(kinetic energy) + 위치에너지(potential enegy)
* 계의 전체적인 운동에 기인되는 것과 같은 운동에너지는 포함하지 않음 (지구의 회전 등)
내부 에너지 변화는 다음과 같이 나타냄
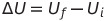
내부 에너지는 계의 현재 상태에만 의존하고 그 상태가 어떻게 이루어졌는가에 대해서는 무관한 상태 함수(state function)
* 상태함수의 반대는 경로함수(path function)으로 그 상태가 어떻게 이루어 졌는가에 의해 달라짐
- 내부 에너지의 분자 수준 해석
# 분자들의 세가지 운동 방식, (= 분자들이 가질 수 있는 자유도, mode 수)
병진 운동(translation) : 공간 속에서의 질량 중심의 이동
질량 중심 주위의 회전(rotation)
진동(vibration) : 질량 중심은 이동하지 않은 채로 결합 길이와 결합 각의 변화
* 이 셋 중 병진 운동과 회전에 의한 운동만 온도에 비례하는 기여를 하며 내부 에너지에 영향을 줌
분자의 물리적 성질이나 화학적 성질은 대부분 이 운동 방식들이 갖는 에너지에 의존함
# 단원자 분자, 다원자 분자의 내부 에너지
기체 분자의 병진 운동(translation)에 의해 기인되는 평균 에너지는 3/2kT
*k와 아보가드로수 Na를 곱하면 기체상수 R이 됨, kNa=R
단원자 분자(monatomic gas) : Um(0)+3/2RT
* 병진 운동에 의한 에너지 3/2RT
선형 다원자 분자(linear polyatomic gas) : Um(0)+3/2RT+RT
* 병진 운동에 의한 에너지 3/2RT + 회전에 의한 에너지 RT, 이때 선형이기 때문에 x,y,z축 중 2개의 자유도를 가짐
비선형 다원자 분자(nonlinear polyatmoic gas) : Um(0)+3/2RT+3/2RT
* 병진 운동에 의한 에너지 3/2RT + 회전에 의한 에너지 3/2RT, 이때 비선형이기 때문에 x,y,z축 3개 모두의 자유도를 가짐
# Um(0)은 무엇인가 ?
Um(0)는 T=0 일 때의 몰 내부 에너지
완전 기체 분자들일 경우 분자간 상호작용이 없으므로 분자들 사이의 거리가 에너지에 영향이 없음
즉 완전 기체의 내부 에너지는 기체가 차지하는 부피에 무관함, Um(0)=0
- 1법칙의 수식화
열역학의 1법칙 : 고립된 계의 내부 에너지는 일정함
이를 수식으로 나타내면 다음과 같음
$ \Delta U=q+w$
3. 팽창 일
변화의 양이 작을 때
$ \Delta U=q+w$
위의 식에서 상태의 미소 변화와 내부 에너지의 미소 변화를 주목하면 다음과 같은 식이 나옴
$dU=dq+dw$
- 일에 대한 일반적 식
팽창 일(expansion work = pv work)은 힘 F가 dz만큼의 거리를 이동했을 때 다음과 같이 정의됨
이때 (-) 부호는 다른 변화가 없다면 이 계의 내부 에너지가 감소된다는 사실을 나타낸 것임
$ dw=Fs=- |F| dz$
dz > 0 이면 dw는 음
dz < 0 이면 dw는 양
단면적을 A, 외부 압력을 Pex라 했을 때,
$F=p_{ex}A$
$ w=- \int_{V_i}^{V_f}{p_{ex}dV}$
Vf>Vi 이면 w는 음
Vf<Vi 이면 w는 양
- 일정 압력에서의 팽창
대기의 압력을 받는 피스톤 등의 과정을 생각해 보면
$ w=-{p_{ex}} \int_{V_i}^{V_f}{dV}=-p_{ex}(v_f-V_i)$

# 자유 팽창(zero opposing force)
자유 팽창이란 맞서는 대립 힘이 0일 때를 말함
즉 Pex=0이고 w=0임
- 가역 팽창(reversible expansion)
가역 변화란 변수를 미소하게 변화시켜서 그 변화를 역방향으로 일어나게 할 수 있는 과정을 말함
가역적 팽창을 일으키려면, 각 팽창 단계마다 외부압력 Pex와 내부압력 p를 같게 해주어야함
만약 외부압력과 내부압력이 크게 다를 경우 과정의 역방향이 일어나지 않는 비가역적 팽창이 일어남
가역 팽창 일은 다음과 같음
$dw=-p_{ex}dV=-pdV$
$w=- \int_{V_i}^{V_f}{pdV} $
여기서 p를 V의 함수로 나나태면 이 적분값을 계산할 수 있음
- 등온 가역 팽창
등온 가역 팽창은 위의 $w=- \int_{V_i}^{V_f}{pdV} $ 식에서 이상기체 방정식 $pV=nRT$ 를 이용함
$w=- nRT\int_{V_i}^{V_f}{ \frac{dV}{V} } =-nRTln \frac{V_f}{V_i} $
$V_f>V_i$ : w는 음수
* 계가 주위에 일을 하며 그만큼 계의 내부 에너지가 감소함
* 하지만 추후에 이를 보충하는 열에너지가 유입되어 전체적 U는 일정함
$V_f<V_i$ : w는 양수
또한 w는 T에관한 함수이기 때문에 같은 부피 변화라 하여도 높은 온도에서 일어날수록 더 많은 일이 행해짐
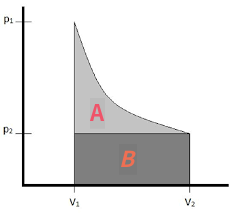
# 가역 과정과 비가역 과정의 한 일

위의 그래프에서
A+B : 등온가역 상태에서의 팽창과 수축이 일어날 때 한 일
B : 비가역적으로 팽창될때(v1에서 v2로) 한 일
팽창 시 각 단계에서 외부 압력을 내부 압력에 맞춰줌으로써 계는 미는 힘을 조금도 낭비시키지 않았기에 가역 과정이 비가역 과정보다 많은 일을 얻을 수 있음
* 비가역 수축일 경우(v2에서 v1으로) 한 일은 p1(v2-v1)에 해당하는 더 큰 직사각형의 넓이로 가역 과정보다 한 일이 많음
4. 열의 출입
일반적인 계의 내부 에너지 변화는 다음과 같음
$dU=dq+dw_{exp}+dw_e$
내부 에너지 변화 = 열의 변화 + 팽창일의 변화 + 비팽창일의 변화
이때 부피를 일정하게 해 준 계는 팽창일을 할 수 없으며 계가 다른 종류의 일도 할 수 없다면 dw=0이 됨
즉 위의 조건에서 다음이 성립함
$dU=dq$
이를 부피 V가 일정하다는 의미의 아래 첨자를 이용하면 다음과 같음
$dU=dq_V$
$ \Delta U=q_V$
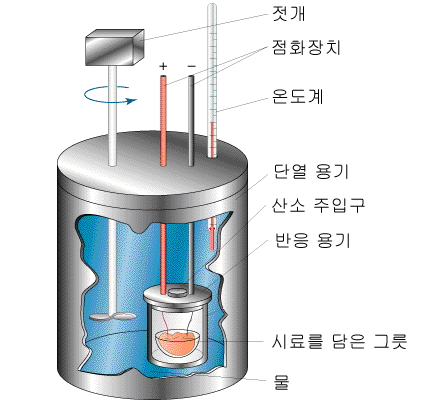
- 열 계량
system마다 열에 대한 맷집이 다르기에 열 계량을 통해 이를 측정할 수 있음
물리적 혹은 화학적 변화가 일어날 때 열로서 이전되는 에너지를 조사하는 것이 열 계량임
보편적으로 $q_v$를 측정하는 데 쓰이는 장치는 단열 반응통 열량계임

열량계의 온도변화 $ \Delta T$는 반응에서 방출되거나 흡수되는 열에너지에 비례하며 이를 이용해 $q_v$와$ \Delta U$를 측정함
$q=C \Delta T$, 이때 C는 열량계 상수
$q=It \Delta \phi $, I는 전류 t는 시간, $\Delta \phi$는 전위차
두 식을 이용해 열량계 상수 C를 구할 수 있음
- 열용량
물질의 양에 따라서 열에 의해 증가하는 내부 에너지의 정도가 달라지므로 열용량을 구할 때는 주로 일정 부피 조건을 사용함
$C_V= \frac{ \Delta q_V}{ \Delta T} =( \frac{ \partial U}{ \partial T})_V $
* $C_V$가 크다는 것은 같은 열 $q_V$로 온도 변화가 작다는 것으로 온도를 올리기 어렵다는 말임
* 상전이 온도에서는 시료의 열용량이 무한대가 되며 아무리 많은 열을 가해 주어도 온도가 올라가지 않음
* 편도함수란 변수가 여러개일 때 하나를 고정 후 미분하는 것
* 여기서는 U,T,V의 함수에서 변수 V를 고정 후 U를 T에 대해 미분하여 열용량 C를 구함

# 열용량의 크기 성질과 세기 성질
열용량은 크기 성질(extensive)로 100g의 물은 1g의 물보다 100배의 열용량을 가짐
일정-부피 몰 열용량 $C_{V,m}=C_V/n$은 1mol 물질의 열용량이며 세기 성질(intensive)임
열용량은 일정부피 계의 내부 에너지 변화를 온도 변화와 연관시키는데 이용함
$dU=C_VdT$
이때 계산의 편의를 위해 $C_V$를 상수 취급하면 다음 식이 나옴
$ \Delta U=C_V \Delta T$
위의 관계식을 이용하면 시료의 열용량을 간단하게 측정할 수 있음
일정량의 열을 시료에 가하고 여기에 기인되는 온도 상승을 나눠주면 시료의 일정-부피 열용량이 나옴
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 2-3 열화학 (0) | 2024.09.05 |
|---|---|
| 【물리화학1】 2-2 엔탈피 (8) | 2024.09.04 |
| 【물리화학1】 2장 열역학 제 1법칙 (2) | 2024.09.03 |
| 【물리화학1】 1장 기체의 성질 목차 (0) | 2024.08.09 |
| 【물리화학1】 1-3 실제 기체 (0) | 2024.08.09 |