1. 드루드 모델의 원리
- 고체 내 전자 혹은 정공의 흐름
표동(Drift)와 확산(Diffusion)으로 나누어짐
표동 : 전기장의 존재에 의해 (-)전하를 가진 전자가 (-)에서 (+)로 이동하는 현상
확산 : 농도차에 의해 전자가 농도가 높은 곳에서 낮은 곳으로 이동하는 현산
- 드루드 모델(Drude Model)
금속 내 전자의 움직임을 설명하는 모델
핀볼처럼 도체 안의 자유 전자가 무한히 단단한 양이온에 부딪치면서 움직이는 것으로 가정
반도체 내 전기장의 존재 하에서 전하의 표동(전자가 이동하는 원리)을 설명함
반도체 내 전기장 E가 존재할 때, 유효질량m을 갖는 전자가 받는 힘 F는 다음과 같음
e: 전하량, v: 전자 속도, τ: 전자의 Relaxation Time(전자의 충돌 이후 다시 충돌이 일어날 때까지 걸리는 평균 시간)
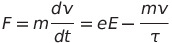
* 전기장 E에 의해 eE의 힘을 갖지만, 반도체 내부 결함, 불순물, 포논 등에 의한 산란 때문에 - 값을 가짐
<전기 전도도 식을 구하기 위한 과정>
정상 상태일때, 평형상태(steady state)에 도달하면 일정한 전류가 흐르게 되고 F가 0이 됨
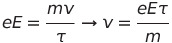
전자 이동도(Electron mobility) 정의
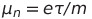
전자의 속도 v가 모든 전자에게 적용된다고 가정하면
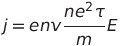
j : 전류의 밀도, n : 전자의 밀도
전류밀도 J
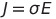
J : 전류의 밀도, σ = 전기전도도, E : 전기장
전기전도도 σ
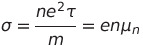
즉 전자의 표동에 의한 전기전도도는 전자의 농도 n과 전자의 이동도 μ에 의해 결정됨
2. MOSFET의 동작 영역
-MOSFET의 동작 영역
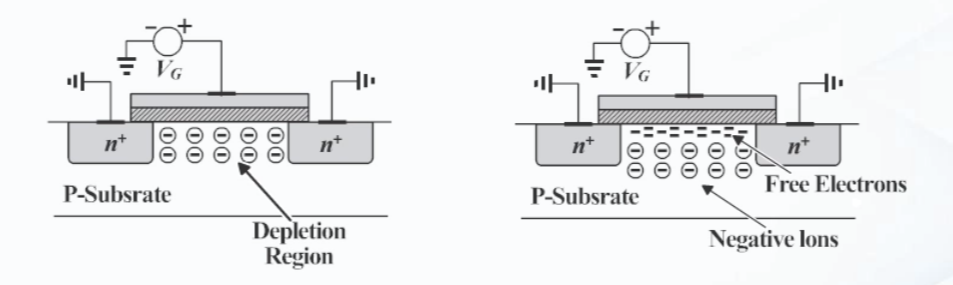
Vg>0 이 되면 공핍영역(Depletion Region)이 생김
Vg>Vth>0V가 되면 p-형 반도체에서 소수캐리어인 전자의 개수가 정공보다 많아지면 Inversion Region이 생기고 채널이 형성됨
* Vth : 문턱전압, 채널이 형성되기 시작하는 전압
- MOSFET의 에너지 밴드
MOSFET의 에너지 밴드는 왼쪽부터 순서대로 Metal, Oxide, Silicon 순서임
왼쪽 그림은 Depletion Region 오른쪽 그림은 Inversion Region을 나타냄
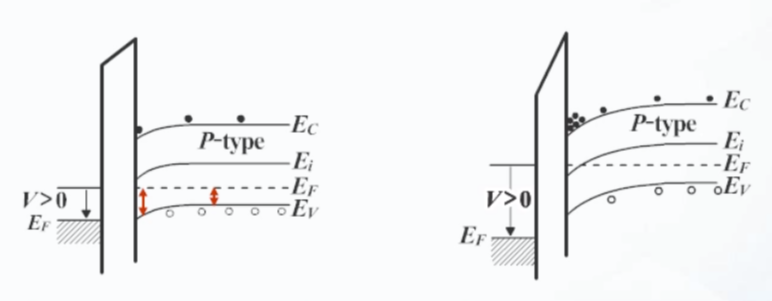
Depletion Region
Metal의 밴드는 내려가고 Silicon의 밴드는 올라감
Ef(페르미 레벨)를 보면 Ev와 멀어져 도핑 농도가 떨어지고 이는 정공을 인위적으로 뺀 것과 같음
즉 전자가 남아 실리콘 표면에 (-)전하를 갖음
Inversion Region
Silicon 에너지 밴드가 계속해서 올라감 Ef(페르미 레벨)이 Ev를 떠나 Ec와 점점 가까워짐
도핑 상태가 반전되는 상황으로 이러한 현상에 의해 실리콘 바디에 채널이 생김
- Inversion Region의 세부 조건
MOS 구조에서 P형 반도체 표면에서의 에너지 밴드임
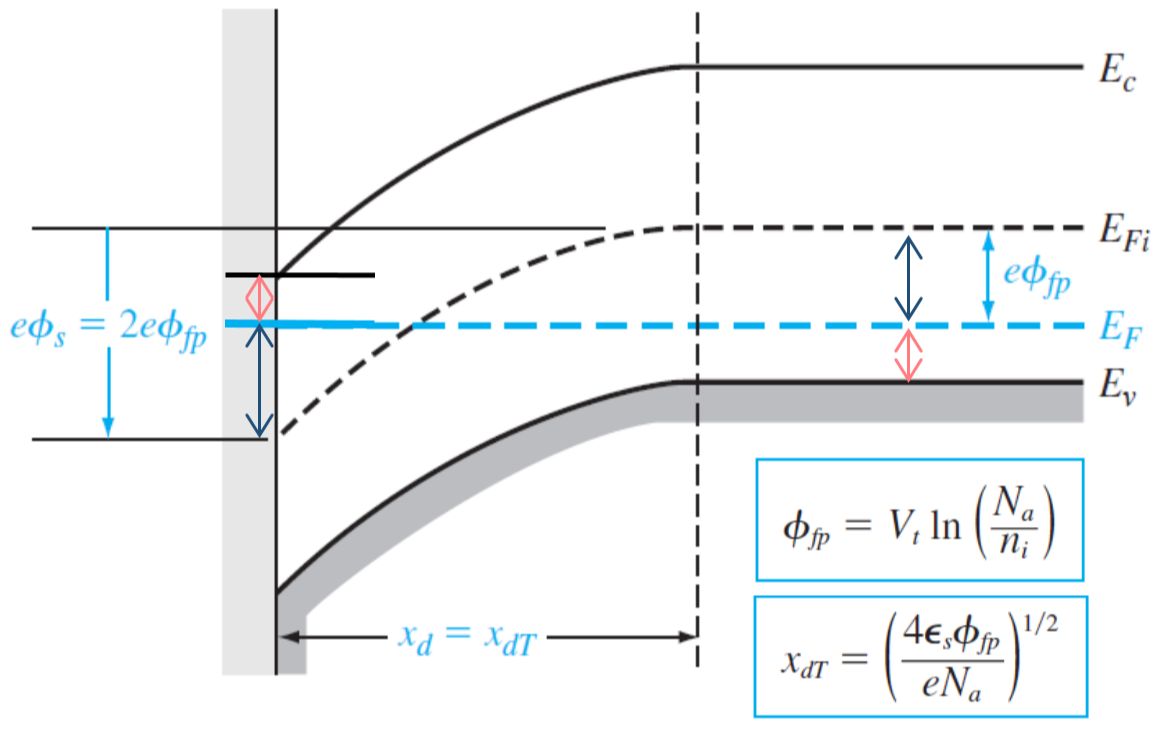
Ei : 반도체 밴드갭의 중간에 해당하는 에너지, Ef : 페르미 레벨
Ψs : 표면전위(Surface Potential)
Ψbp: Ei-Ef
Ψs>Ψbp : Inversion 현상이 일어나기 시작하는 조건
Ψs>2Ψbp : Strong Inversion 현상이 일어나는 조건
Vg가 양의 방향으로 증가할 때, 표면전위가 양의 방향으로 상승하고, Ψbp보다 표면전위가 커질때 Inversion이 일어남
- 전류-전압 특성(I-V Characteristics) 유도
자세한 유도는 다음 블로그 참조 https://blog.naver.com/tmddls4562/221970681088
MOSFET의 전류-전압 공식
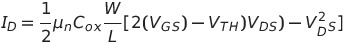
- 동작 영역에 따른 전류-전압 공식의 변화
드레인 전류 Id : 전자 이동도 μ, 게이트 커패시턴스, W/L 에 비례함
* 다른 값은 고정인데 이동도 μ 가 높다면 같은 면적에서 더 큰 전류가 만들어질 수 있음
* 게이트 커패시턴스 : 전하 농도와 관련된 값으로 더 큰 게이트 커패시턴스는 더 큰 전자 농도를 갖게 하며 더 큰 전류를 만들어냄
* W/L : 종횡비의 역수로 소자의 폭/높이임, 이를 크게하면 전류도 커지며 병렬 방향으로 많은 MOSFET 집적가능해짐
이때 Vds가 Vgs-Vth보다 클 때와 작을 때 각각 Saturation Region과 Triode Region으로 나뉨
선형영역(Triode Region) Vds < Vgs - Vth 일때 전류의 식
Vds << 2(Vgs - Vth) 이므로
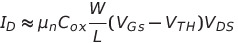
Id와 Vds는 선형적으로 비례함
포화영역(Saturation Region) : Vds >= Vgs - Vth 일때 전류의 식
Vds = Vgs-Vth
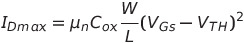
Id와 Vds는 상수관계임
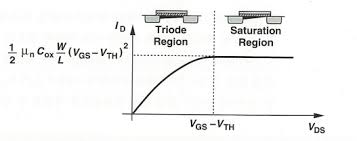
하지만 실제로는 포화영역(Saturation Region)에서도 Vds가 증가하게 되면 일정 비율로 Id도 증가함
- 포화영역에서의 전류-전압 특성 변화
포화영역에서 전압 증가에 따른 전류 증가 현상으로 채널 길이 변조 현상이 발생함
Pinch-off 현상에 의해 Vds >= Vgs-Vth 조건에서 유효 채널의 길이가 짧아지게 되어 L이 L1으로 줄음
따라서 Vds가 증가할수록 유효채널 L1이 감소하며 Id는 증가함
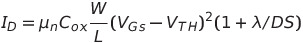
λ : 채널 길이 변조 개수, 이것에 의해 포화영역에서의 I-V 기울기가 결정됨
3. 트랜스컨덕턴스(Transconductance)
- 트랜스 컨덕턴스(Transconductance), gm
MOSFET은 gm 파라미터에 의해 성능이 결정됨
gm이 크다는 것은 작은 전압으로도 큰 전류 변화를 유도할 수 있다는 것
이를 이용하여 다른 MOSFET 반도체 소자의 성능을 비교가능함
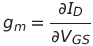
이를 계산하면
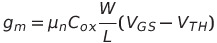
Vgs - Vth 값이 고정 : 이동도, 게이트 커패시턴스, W/L 과 비례
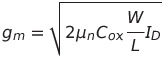
전류 Id가 고정 : 이동도, 게이트 커패시턴스, W/L의 Square Root에 비례
4. 이동도(Mobility), μ
- 이동도, μ 추출
MOSFET의 gm과 이동도 μ는 비례함
MOSFET 전류공식에서 이동도 μ를 정리할 수 있음
선형영역에서 이동도 μ 추출
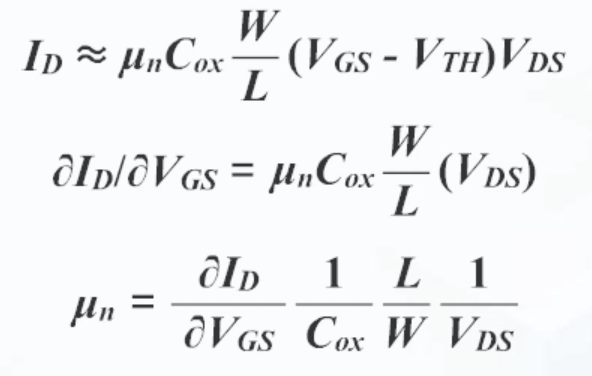
포화영역에서 이동도 μ 추출
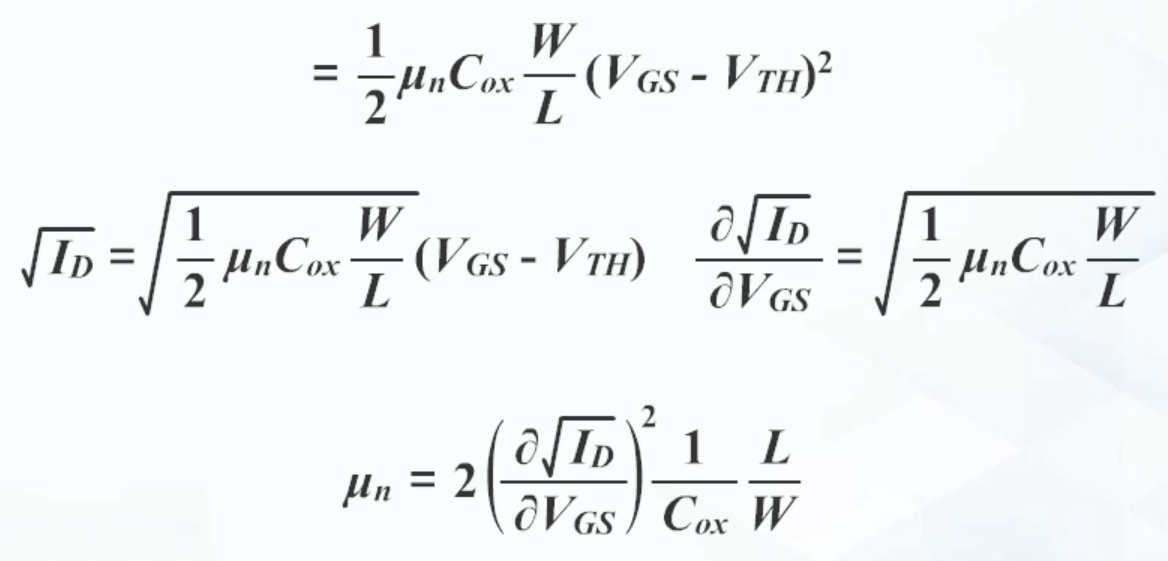
5. 문턱전압(Threshold Voltage)
- 문턱전압 Vth 추출
MOSFET의 gm과 Id에 직접적으로 영향의 미치는 값은 Overdrive Voltage, Vov-Vgs-Vth 임
Vth를 추출하기위한 방법은 Linear Extrapolation Method, Second-derivative Metohd, Constant-current Method 등이 있음
'공부 > 【반도체 공정】' 카테고리의 다른 글
| 【반도체 제조 개론】 5강 - 실리콘 웨이퍼의 필요성 (0) | 2024.05.24 |
|---|---|
| 【반도체 제조 개론】 4강 - 차세대 반도체 단위 소자의 특징과 종류 (0) | 2024.05.20 |
| 【반도체 제조 개론】 2강 - 반도체 단위 소자의 기본 구조 및 동작 원리 (0) | 2024.05.17 |
| 【반도체 제조 개론】 1강 - 반도체 분야와 개념 이해하기 (0) | 2024.05.16 |
| 【반도체 제조 개론】 0주차 - 목차 (0) | 2024.05.16 |