기체 분자 운동론은 기체 에너지는 분자의 kinetic energy에 의해서만 생성된다고 가정함
1. 분자 운동론
분자 운동 모형은 다음 세 가지 가정을 전제로 함
● 기체는 고전역학의 법칙을 따르면서 연속적인 무작정 운동을 하는 질량이 m인 분자로 되어 있다.
● 이 분자들은 상호 충돌 사이에 날아가는 평균 거리에 비해서 대단히 작은 지름을 가지고 있으며, 이런 면에서 그 크기를 무시할수 있다.
● 이 분자들은 순간적인 탄성 충돌을 할 때만 상호작용을 함
- 압력과 분자 속력
압력은 기체분자가 벽을 두드리는 정도
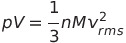
이때 Vrms는 분자의 속력 v의 제곱을 평균한 다음에 제곱근을 취한 근 제곱 속력임
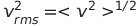
- 위의 식의 간단한 증명
분자는 무작위 운동을 하므로 x축과 평행한 성분을 기준으로 둠
질량이 m인 알맹이가 오른쪽 기벽과 충돌할 때 운동량은 충돌 전 mv에서 충돌 후 -mv로 2mv만큼 변함
*x축으로의 속도인 v_x를 편의상 v로 사용
Δt의 시간동안 기벽과 충돌하며 운동량의 총 변화는 각 분자의 운동량 변화에다 그 시간 동안에 기벽에 접근하는 분자수를 곱한 것임
기벽의의 넓이를 A라고 하면 알맹이가 vΔtA의 부피 속에 들어있는 알맹이가 기벽과 충돌함
부피 당 알맹이의 수는 nN_A/V
*N_A는 아보가드로 수
이때 절반은 오른쪽으로 향하고 절반은 왼쪽으로 향해 알맹이 중 절반은 기벽과 충돌하지 못할 것임
따라서 운동량 변화는 다음과 같음
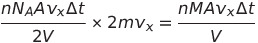
이때 운동량의 시간의 변화율, 즉 시간으로 미분한 값이 힘 (뉴턴의 운동의 제 2법칙에 의해서)
단위 넓이에 작용하는 힘, F/A가 바로 압력임
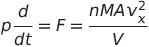
*이때 p는 운동량
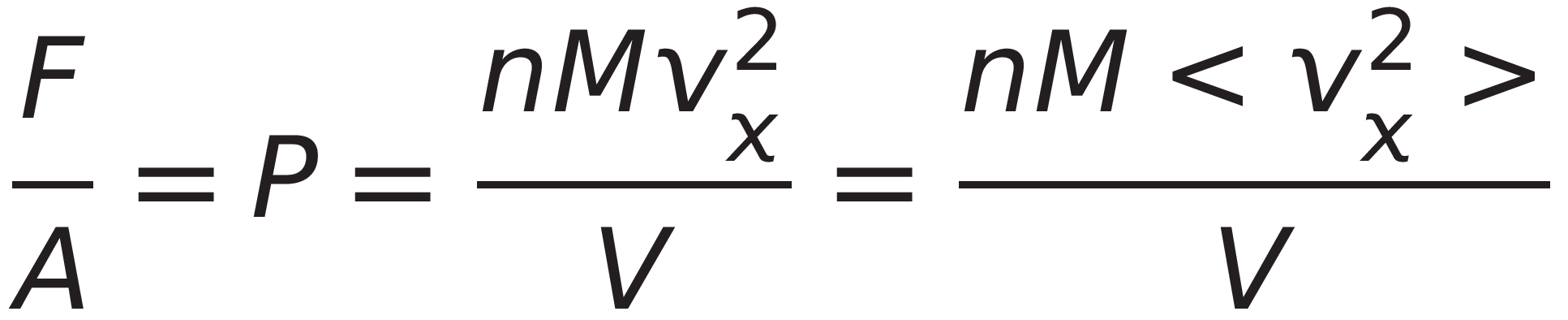
* 분자들이 사실 모두 동일한 속도로 움직이는게 아니므로 압력 p는 평균값으로 계산됨
이때
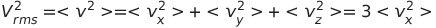
* 분자들은 무작정하게 움직이므로 이들 세 평균치는 모두 동일함
★위 식을 이용하면 다음 식을 유도할 수 있음★
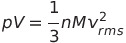
* 만약 위 식에서 근 평균 제곱 속력이 온도에만 의존한다면 일정한 온도에서 'pV = 일정'이 되어 Boyle의 법칙이 성립함
* 완전 기체 상태식이 되려면 우변이 nRT와 같아야 하므로 다음과 같은 식이 성립함
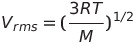
- Maxwell-Boltzmann 속력 분포
실제 기체에 있어서 개개 분자들의 속력은 넓은 범위에 걸쳐 퍼져 있고 분자들 간의 충돌로 이 속력들이 끊임 없이 재분배됨
이러한 기체의 특성을 반영한 식이 Maxwell-Boltzmann 속력 분포임
적분을 통해 Vrms, Vmean, Vmp, Vrel 을 계산할 수 있음
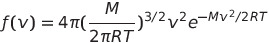
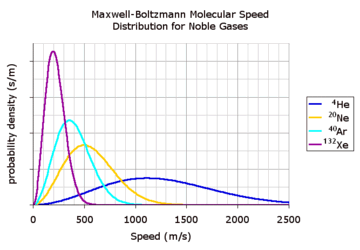
낮은 온도, 높은 분자 질량의 분포 함수는 가파르게, 높은 온도, 낮은 분자 질량의 분포함수는 완만하게 분포함
- Maxwell 분포함수를 이용한 평균치의 계산 (Vmean, Vrms, Vmp, Vrel 등)
Maxwell-Boltzmann 분포 함수를 적분하면 V^n의 평균치를 계산할 수 있음
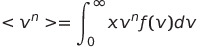
이때 n=2를 넣으면 다음과 같은 식이 나옴
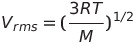
n=1일때
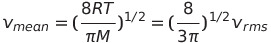
가장 잦은 속력 Vmp는 봉우리의 위치로부터 구할 수 있음
*mp는 most probable speed의 약자, 분포함수를 미분해서 극값을 구하면 됨
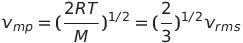
분포함수를 이용하여 한 분자가 다른 분자에 접근하는 평균속력, 즉 상대적 평균 속력 Vrel도 계산할 수 있음
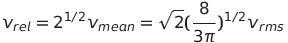
* 일반적인 평균 접근 방향은 직각의 측면으로부터이며 이때 평균 접근 속력을 계산한 것
2. 분자 충돌
분자들이 충돌하는 빈도와 충돌 사이에 평균적으로 이동하는 거리를 계산
- 충돌 빈도
한 분자를 제외한 모든 분자들의 위치를 동결시킴
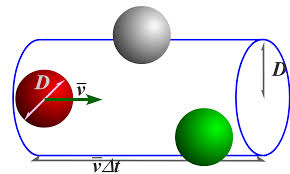
한 분자가 Δt 시간동안 Vrel로 기체 속을 통과할 때 생기는 원통 속에 위치한 정지 상태의 분자들의 수 = 충돌 빈도
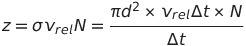
* d는 분자 지름, N은 알맹이 수 밀도
완전 기체 상태식을 이용하면 기체 압력으로도 나타낼 수 있음
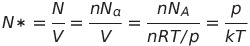
* k는 볼츠만 상수(R/Na), N*은 알맹이 수 밀도
- 평균 자유 행로
충돌 빈도를 통해 충돌 안하는 거리인 평균 자유 행로, mean free path를 구할 수 있음
이를 통해 충돌 안하는 시간도 계산 가능
한 분자의 충돌 빈도가 z라면 1/z 동안에는 충돌을 하지 않고 자유 비행을 할 것임
따라서 1/z*Vrel 만큼의 거리를 날아갈 것임
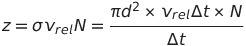
위 식을 이용하면 다음과 같은 식을 유도할 수 있음
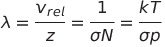
압력을 배로 증가시키면 평균 자유 행로는 반이됨
* 위의 평균 자유 행로식에 T가 들어있지만, 압력p가 T에 비례하므로 T/p는 변하지 않고 일정함
* 비행거리는 부피 속에 들어있는 분자들의 수에 의해서 결정됨
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 2장 열역학 제 1법칙 (2) | 2024.09.03 |
|---|---|
| 【물리화학1】 1장 기체의 성질 목차 (0) | 2024.08.09 |
| 【물리화학1】 1-3 실제 기체 (0) | 2024.08.09 |
| 【물리화학1】 1-1 완전 기체 (0) | 2024.07.06 |
| 【물리화학1】 0장 목차 (0) | 2024.07.06 |
기체 분자 운동론은 기체 에너지는 분자의 kinetic energy에 의해서만 생성된다고 가정함
1. 분자 운동론
분자 운동 모형은 다음 세 가지 가정을 전제로 함
● 기체는 고전역학의 법칙을 따르면서 연속적인 무작정 운동을 하는 질량이 m인 분자로 되어 있다.
● 이 분자들은 상호 충돌 사이에 날아가는 평균 거리에 비해서 대단히 작은 지름을 가지고 있으며, 이런 면에서 그 크기를 무시할수 있다.
● 이 분자들은 순간적인 탄성 충돌을 할 때만 상호작용을 함
- 압력과 분자 속력
압력은 기체분자가 벽을 두드리는 정도
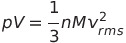
이때 Vrms는 분자의 속력 v의 제곱을 평균한 다음에 제곱근을 취한 근 제곱 속력임
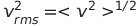
- 위의 식의 간단한 증명
분자는 무작위 운동을 하므로 x축과 평행한 성분을 기준으로 둠
질량이 m인 알맹이가 오른쪽 기벽과 충돌할 때 운동량은 충돌 전 mv에서 충돌 후 -mv로 2mv만큼 변함
*x축으로의 속도인 v_x를 편의상 v로 사용
Δt의 시간동안 기벽과 충돌하며 운동량의 총 변화는 각 분자의 운동량 변화에다 그 시간 동안에 기벽에 접근하는 분자수를 곱한 것임
기벽의의 넓이를 A라고 하면 알맹이가 vΔtA의 부피 속에 들어있는 알맹이가 기벽과 충돌함
부피 당 알맹이의 수는 nN_A/V
*N_A는 아보가드로 수
이때 절반은 오른쪽으로 향하고 절반은 왼쪽으로 향해 알맹이 중 절반은 기벽과 충돌하지 못할 것임
따라서 운동량 변화는 다음과 같음
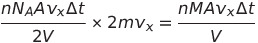
이때 운동량의 시간의 변화율, 즉 시간으로 미분한 값이 힘 (뉴턴의 운동의 제 2법칙에 의해서)
단위 넓이에 작용하는 힘, F/A가 바로 압력임
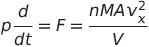
*이때 p는 운동량
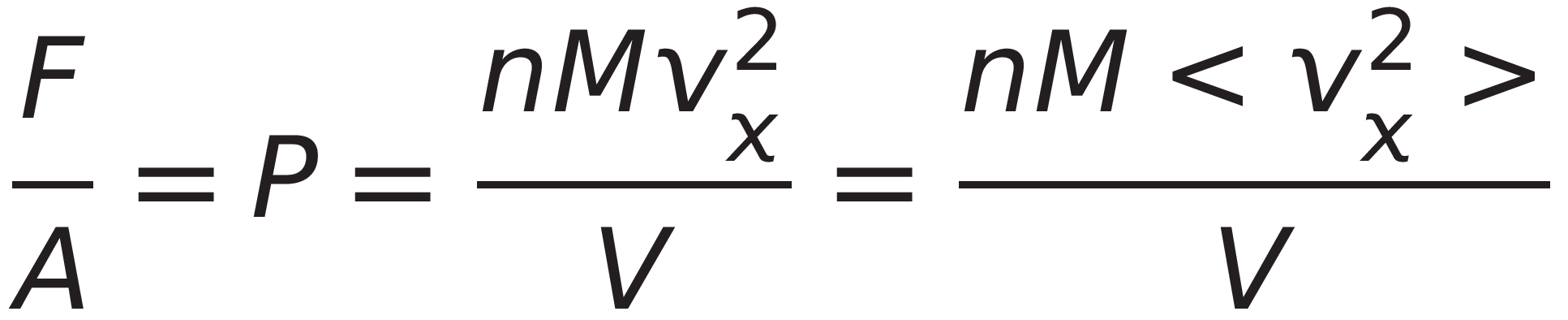
* 분자들이 사실 모두 동일한 속도로 움직이는게 아니므로 압력 p는 평균값으로 계산됨
이때
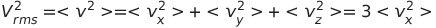
* 분자들은 무작정하게 움직이므로 이들 세 평균치는 모두 동일함
★위 식을 이용하면 다음 식을 유도할 수 있음★
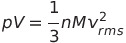
* 만약 위 식에서 근 평균 제곱 속력이 온도에만 의존한다면 일정한 온도에서 'pV = 일정'이 되어 Boyle의 법칙이 성립함
* 완전 기체 상태식이 되려면 우변이 nRT와 같아야 하므로 다음과 같은 식이 성립함
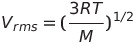
- Maxwell-Boltzmann 속력 분포
실제 기체에 있어서 개개 분자들의 속력은 넓은 범위에 걸쳐 퍼져 있고 분자들 간의 충돌로 이 속력들이 끊임 없이 재분배됨
이러한 기체의 특성을 반영한 식이 Maxwell-Boltzmann 속력 분포임
적분을 통해 Vrms, Vmean, Vmp, Vrel 을 계산할 수 있음
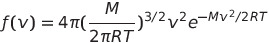
낮은 온도, 높은 분자 질량의 분포 함수는 가파르게, 높은 온도, 낮은 분자 질량의 분포함수는 완만하게 분포함

- Maxwell 분포함수를 이용한 평균치의 계산 (Vmean, Vrms, Vmp, Vrel 등)
Maxwell-Boltzmann 분포 함수를 적분하면 V^n의 평균치를 계산할 수 있음
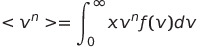
이때 n=2를 넣으면 다음과 같은 식이 나옴
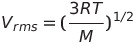
n=1일때
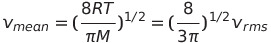
가장 잦은 속력 Vmp는 봉우리의 위치로부터 구할 수 있음
*mp는 most probable speed의 약자, 분포함수를 미분해서 극값을 구하면 됨
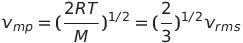
분포함수를 이용하여 한 분자가 다른 분자에 접근하는 평균속력, 즉 상대적 평균 속력 Vrel도 계산할 수 있음
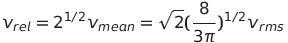
* 일반적인 평균 접근 방향은 직각의 측면으로부터이며 이때 평균 접근 속력을 계산한 것
2. 분자 충돌
분자들이 충돌하는 빈도와 충돌 사이에 평균적으로 이동하는 거리를 계산
- 충돌 빈도
한 분자를 제외한 모든 분자들의 위치를 동결시킴
한 분자가 Δt 시간동안 Vrel로 기체 속을 통과할 때 생기는 원통 속에 위치한 정지 상태의 분자들의 수 = 충돌 빈도
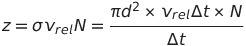
* d는 분자 지름, N은 알맹이 수 밀도

완전 기체 상태식을 이용하면 기체 압력으로도 나타낼 수 있음
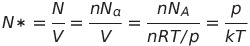
* k는 볼츠만 상수(R/Na), N*은 알맹이 수 밀도
- 평균 자유 행로
충돌 빈도를 통해 충돌 안하는 거리인 평균 자유 행로, mean free path를 구할 수 있음
이를 통해 충돌 안하는 시간도 계산 가능
한 분자의 충돌 빈도가 z라면 1/z 동안에는 충돌을 하지 않고 자유 비행을 할 것임
따라서 1/z*Vrel 만큼의 거리를 날아갈 것임
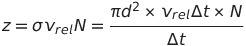
위 식을 이용하면 다음과 같은 식을 유도할 수 있음
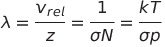
압력을 배로 증가시키면 평균 자유 행로는 반이됨
* 위의 평균 자유 행로식에 T가 들어있지만, 압력p가 T에 비례하므로 T/p는 변하지 않고 일정함
* 비행거리는 부피 속에 들어있는 분자들의 수에 의해서 결정됨
'공부 > 【물리화학1】' 카테고리의 다른 글
| 【물리화학1】 2장 열역학 제 1법칙 (2) | 2024.09.03 |
|---|---|
| 【물리화학1】 1장 기체의 성질 목차 (0) | 2024.08.09 |
| 【물리화학1】 1-3 실제 기체 (0) | 2024.08.09 |
| 【물리화학1】 1-1 완전 기체 (0) | 2024.07.06 |
| 【물리화학1】 0장 목차 (0) | 2024.07.06 |