【화공유체역학】 화공유체역학 기초

1. 유체의 정의

 

유체(Fuild)란 전단응력(Shear Stress)을 지지하지 못하는 물질로, 어떠한 전단응력이 가해지면 변형되는 특성을 가짐

 

- 전단응력(Shear Stress)과 응력(Stress)

 

응력(Stress)은 물체가 변형을 저항하기 위해 생성하는 내부 저항력의 단위 면적당 크기

*압력(Pressure) = 힘(F) / 면적(A) 

응력은 수직응력(Normal Stress)과 전단응력(Shear Stress)으로 구분됨

 

수직응력: 벽면을 누르는 힘, 면에 수직하고 길이, 면적, 체적을 변화시킴

전단응력: 벽면을 스치듯 작용하는 힘, 면에 평행하고 형상(각도)을 변화시킴

 

2. 유체역학의 기본개념

 

- 제어체적(Control Volume, CV)

 

관심 있는 특정 유체 영역을 제어체적으로 설정하여 분석함

 

- 스케일(Scale) 

 

미시적 관점(Microscopic): 국소적인 유체 변화 분석 

거시적 관점(Macroscopic): 전체적인 유체 거동 분석 

 

예시: 밀도의 변화를 측정할 때, 미시적 관찰자는 밀도가 변하는 그래프를 도출하지만 거시적 관찰자는 밀도가 일정한 것으로 본다.

 

- 속도(Velocity)

 

속도는 위치 변화율, 즉 단위 시간당 위치의 변화량을 의미함

 

유체역학에서는 유량(Flow Rate, Q)을 다음과 같이 표현함

 

부피 유량(Volume Flow Rate)  $Q = V \times A$

질량 유량(Mass Flow Rate)  $ \rho Q = m $

운동량 유량(Momentum Flow Rate) $ \rho V^2 A $

 

- 플럭스(Flux) 

 

단위 시간당 단위 면적을 통과하는 양으로 정의됨

유체역학에서는 부피, 질량, 운동량에 대해 적용할 수 있음

 

부피 $ Q/A = V $

질량 $ \rho Q/A = \rho V $

운동량 $ \rho V^2 $

 

3. 점성(Viscosity) 

유체의 흐름에 대한 저항(Resist to Flow)을 의미함

같은 전단응력이 가해졌을 때, 점성이 낮은 물질(예: 물)은 빠르게 흐르고, 점성이 높은 물질(예: 꿀)은 천천히 흐름

 

- 뉴턴 유체(Newtonian Fluid) vs. 비뉴턴 유체(Non-Newtonian Fluid)

 

뉴턴 유체: 전단응력이 속도 구배(velocity gradient)에 대해 선형적으로 증가함, 즉 점성이 일정함

비뉴턴 유체: 점성이 일정하지 않고, 속도 구배에 따라 변함

 

4. 베르누이 방정식(Bernoulli Equation)

 

역학적 에너지 보존 법칙을 유체에 적용한 식

기본 에너지 보존식: $Fs + \frac{1}{2}mV^2 + mgh = 일정 $   

단위: J (줄)

 

 

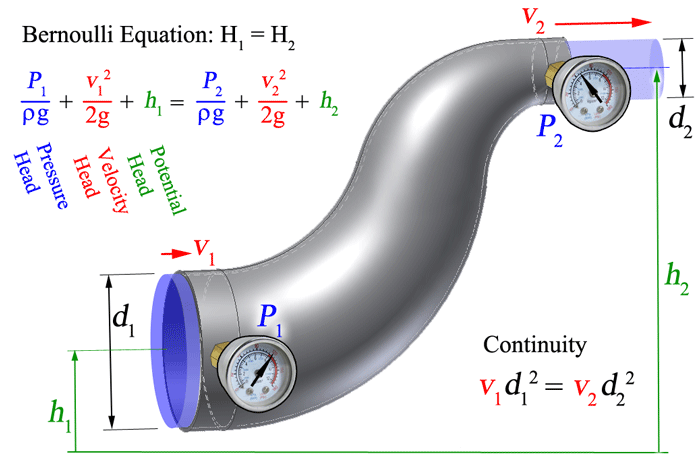
- 유체역학에서의 변형

 

양변을 부피(Volume)로 나누면: $P + \frac{1}{2} \rho V^2 + \rho gh = 일정$

단위: Pa (압력)

각각 세 변수를 정압, 동압, 위치압으로 부름

 

비중량 $ \gamma = \rho g $으로 나누면: $ \frac{P}{\rho g} + \frac{V^2}{2g} + h = 일정 $

단위: m (길이)

각각 세 변수를 압력수두(Pressure Head), 속도수두(Velocity Head), 위치수두(Elevation Head)로 부름

 

이때 계산문제를 풀때는 양변을 부피로 나눈

$P + \frac{1}{2} \rho V^2 + \rho gh = 일정 $ 식을 일반적으로 사용함